[알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386)
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
최소 신장 트리(MST)

최소 신장 트리란 가중치가 있는 무방향 그래프에서 모든 노드를 연결할 때 사용된 엣지들의 가중치의 합을 최소(최소 비용)로 연결 하는 트리 입니다.
무방향의 모든 그래프를 연결할 때, 최소 비용으로 연결하는 트리 입니다.!
특징
- 사이클이 포함되면 가중치의 합이 최소가 될 수 없기 때문에 사이클을 포함하지 않습니다.
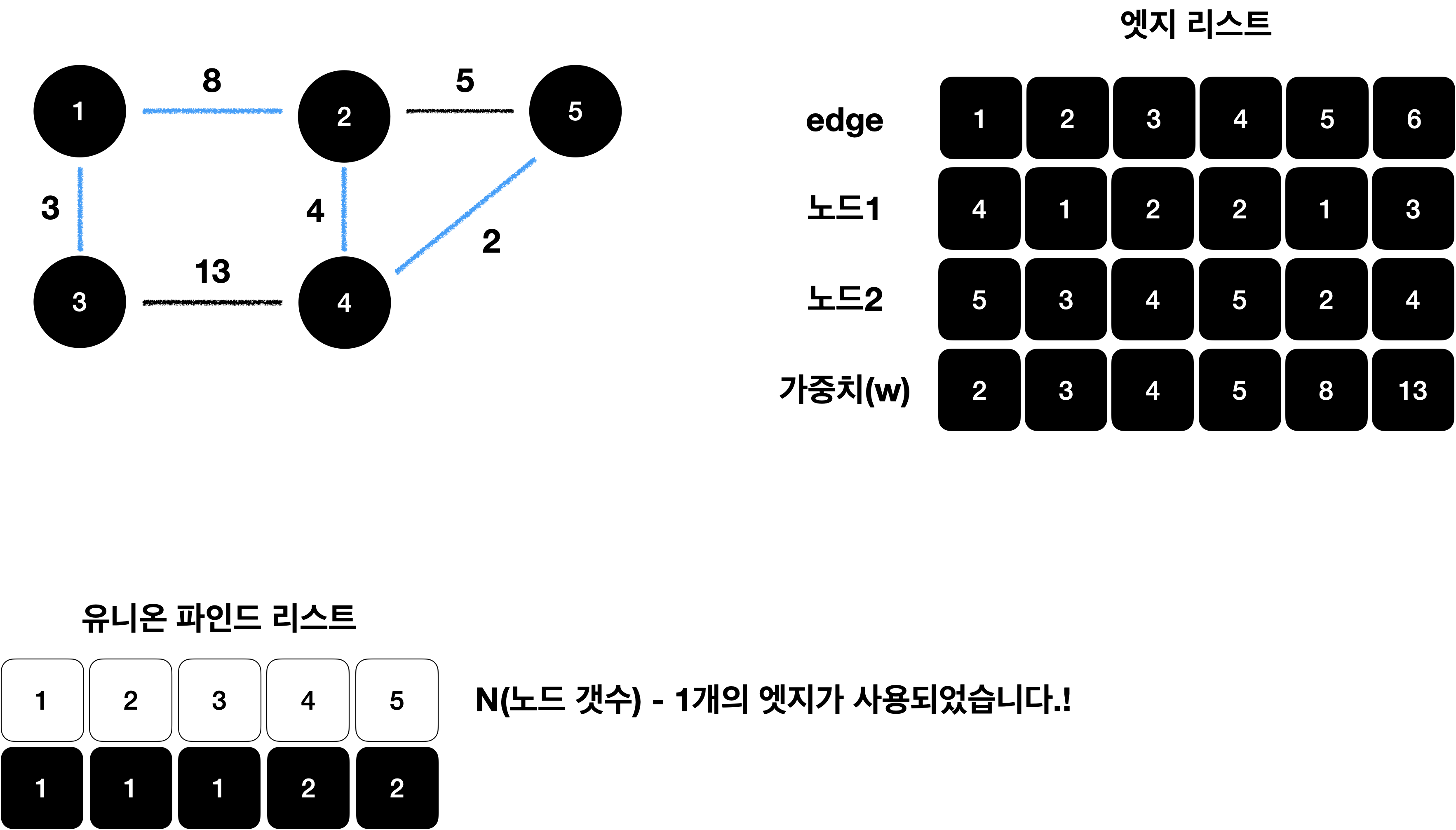
- N개의 노드가 있으면 최소 신장 트리를 구성하는 엣지의 갯수는 항상 N-1개 입니다.

최소 신장 트리 핵심 이론
엣지 리스트로 그래프를 구현하고 유니온 파인드 리스트 초기화
최소 신장 트리는 데이터를 노드가 아닌 엣지 중심으로 저장합니다. 따라서 엣지 리스트의 형태로 저장합니다.
이때 사이클 판단을 위한 유니온 파인드 리스트도 함께 초기화 합니다.

엣지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬합니다.
오름차순으로 정렬해야 최소 비용으로 연결할 수 있습니다.

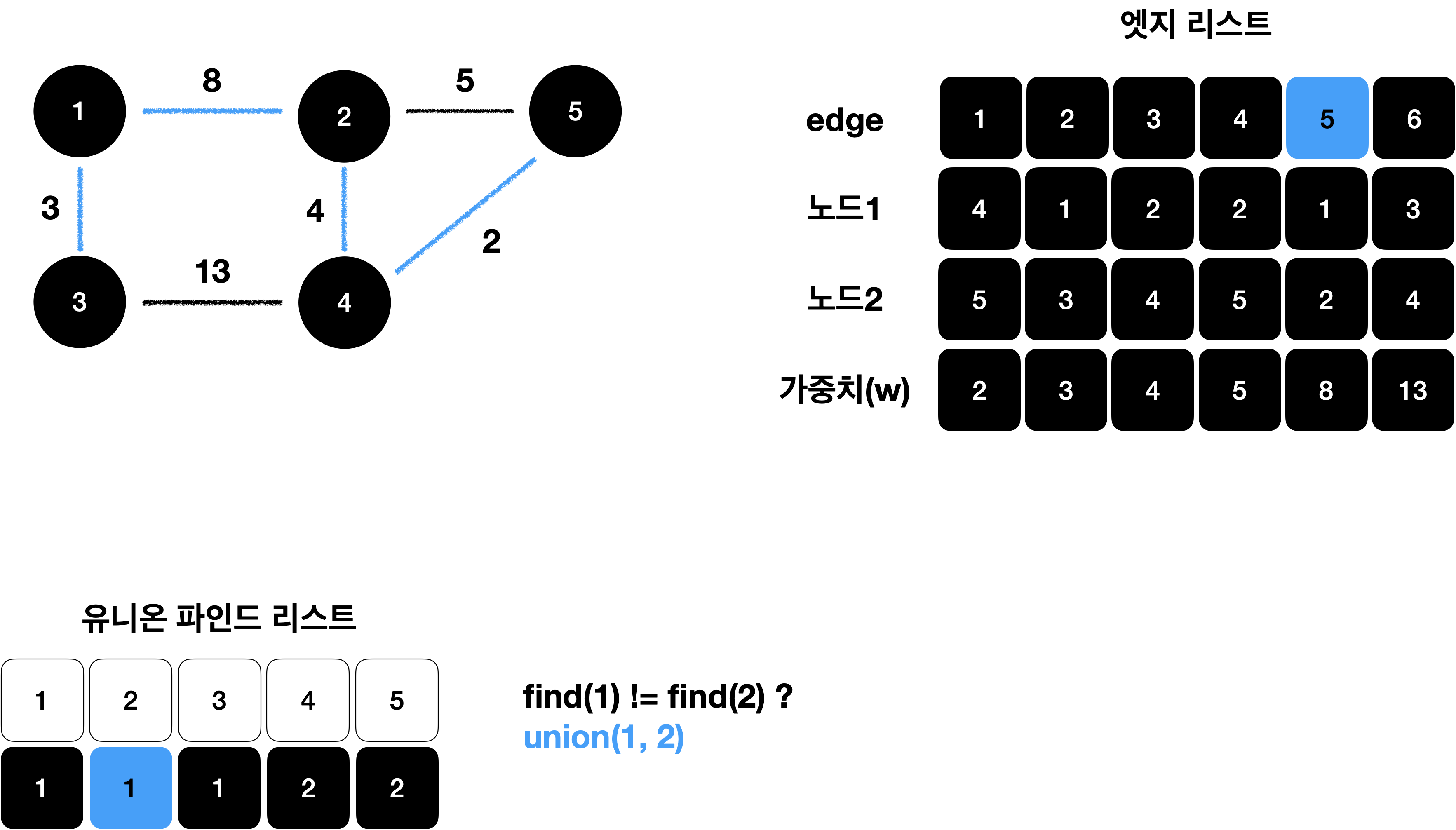
가중치가 낮은 엣지부터 연결
가중치가 낮은 엣지부터 순서대로 선택하여 연결을 시도 합니다.
이때 바로 연결하지 않고,
해당 엣지로 연결했을 때 그래프에 사이클 형성 유무를 find 연산을 통해 확인한 후
사이클이 형성되지 않을 때만 union 연산을 이용하여 노드를 연결 합니다.
(사이클을 포함하면 안되기 때문 입니다.^^)
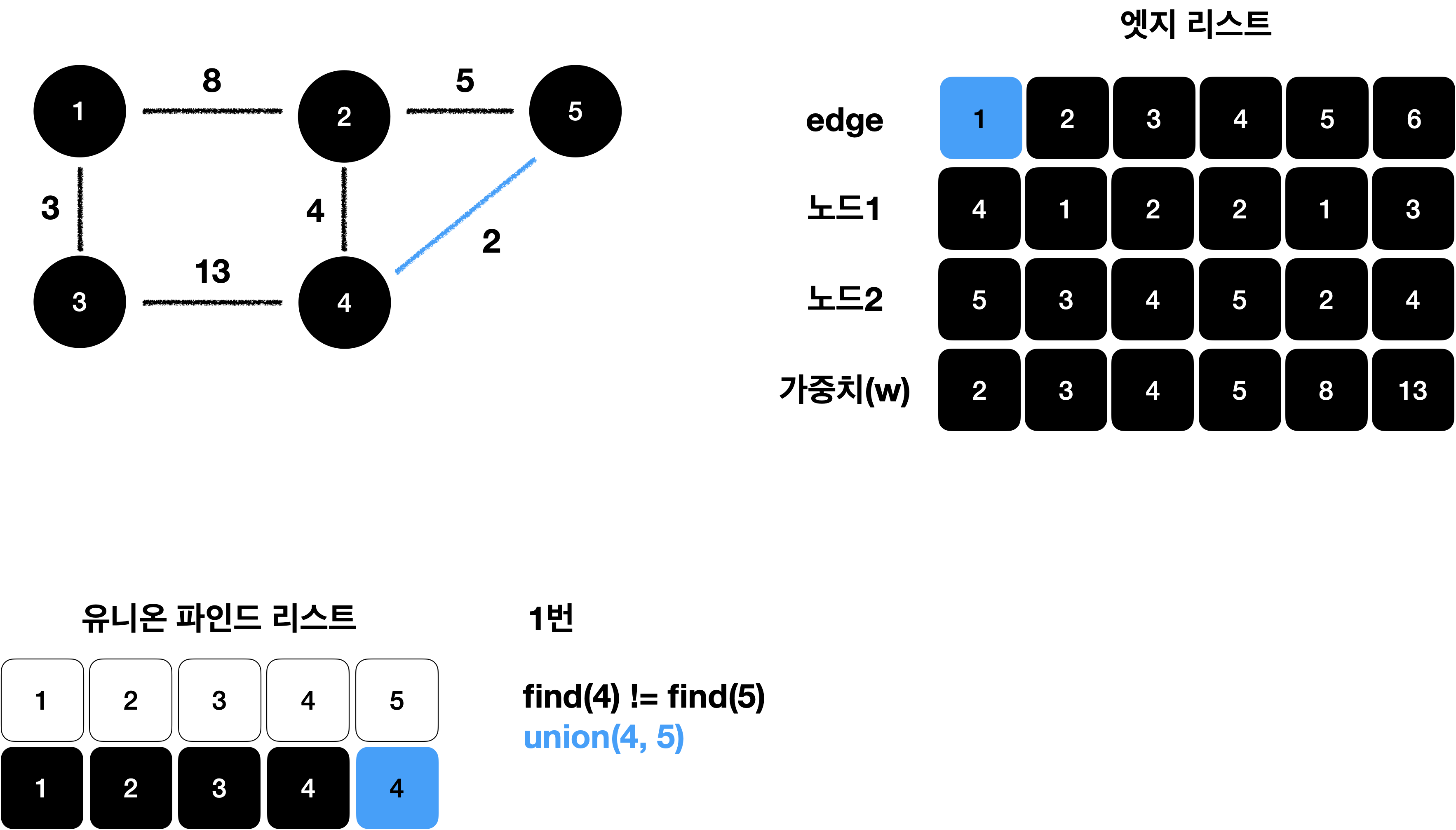
이 과정을 4(N-1)번 반복 합니다.
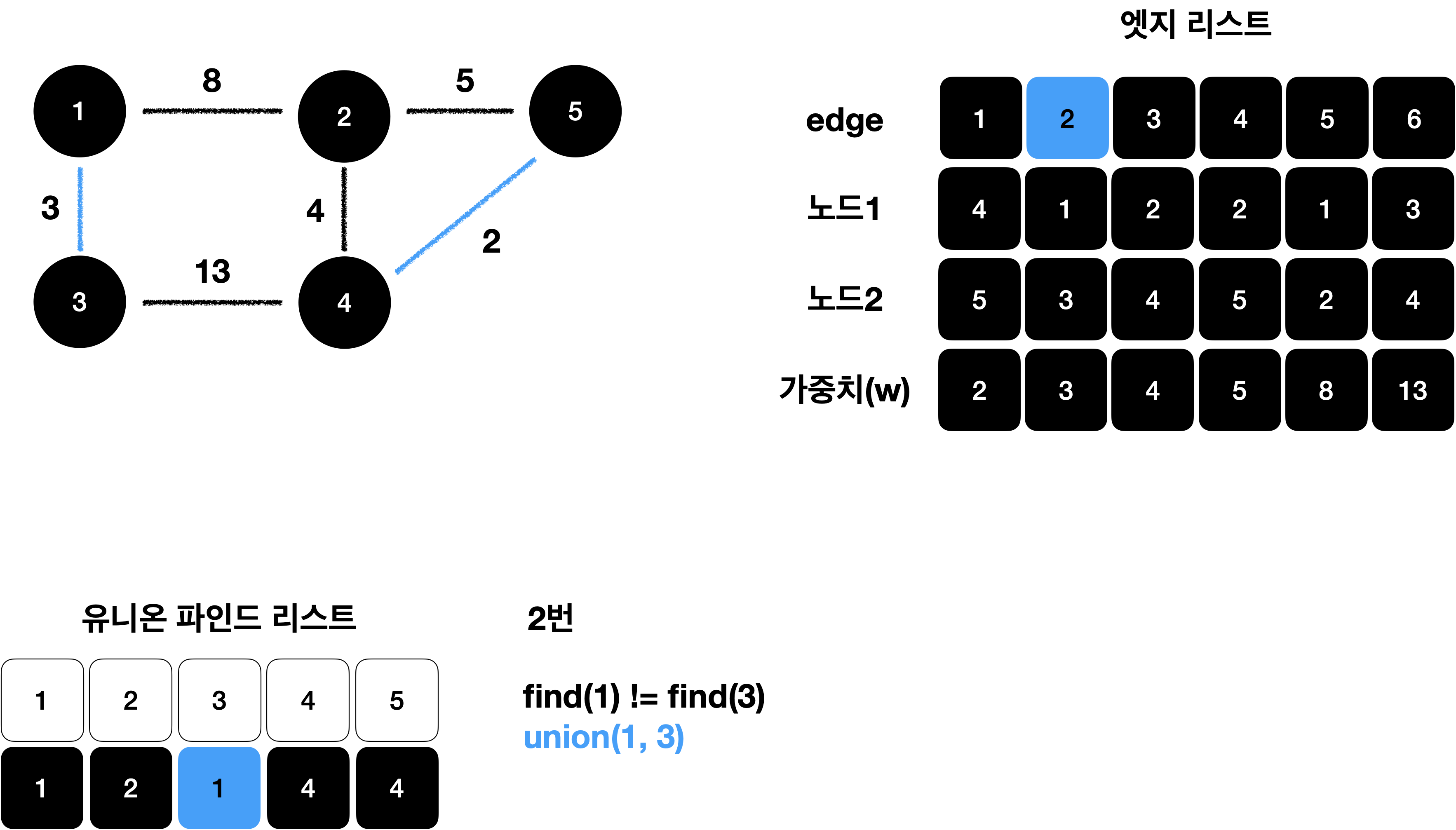
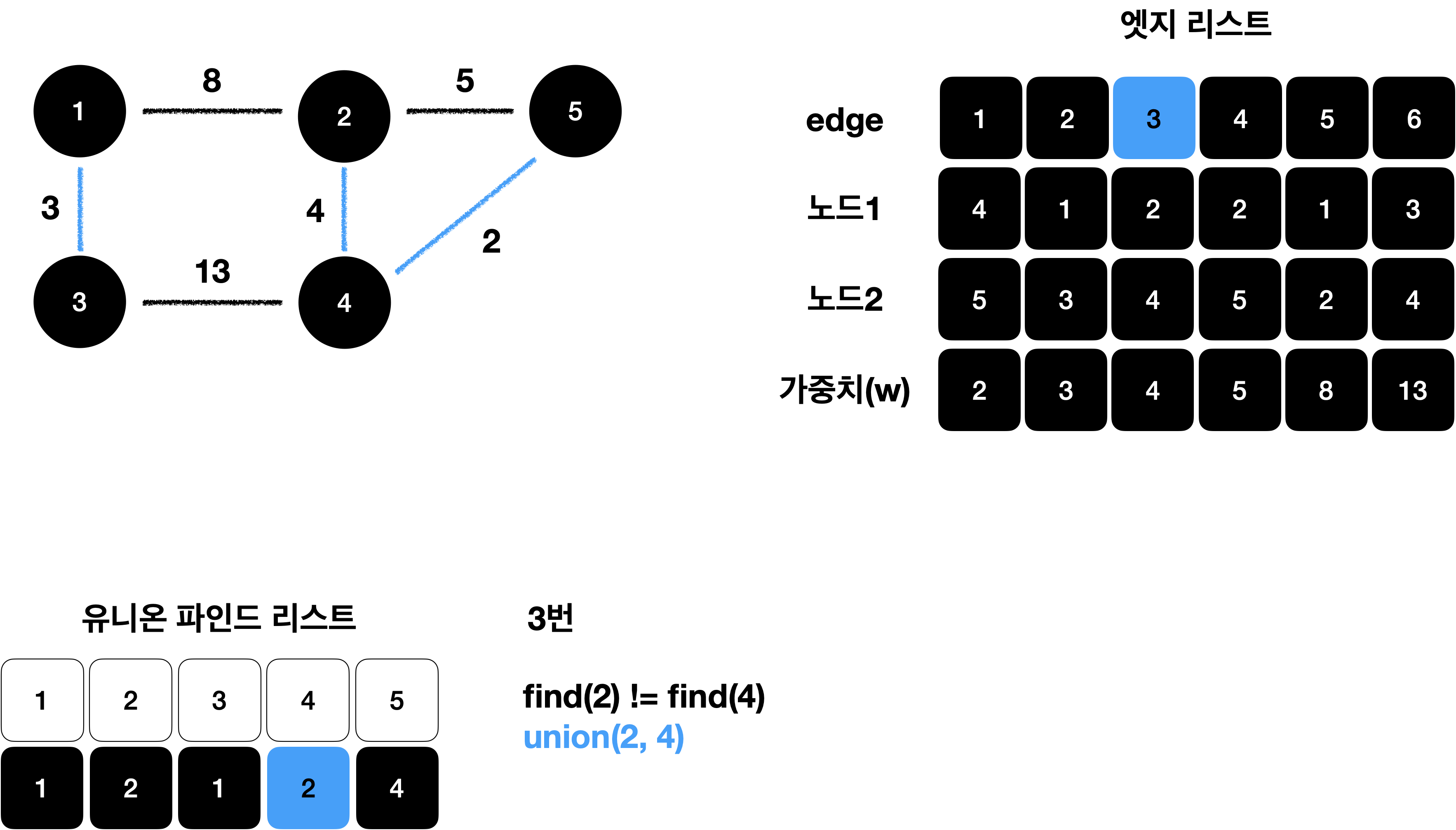
find 연산을 통해 사이클 처리를 하고 대표노드를 업데이트 합니다.
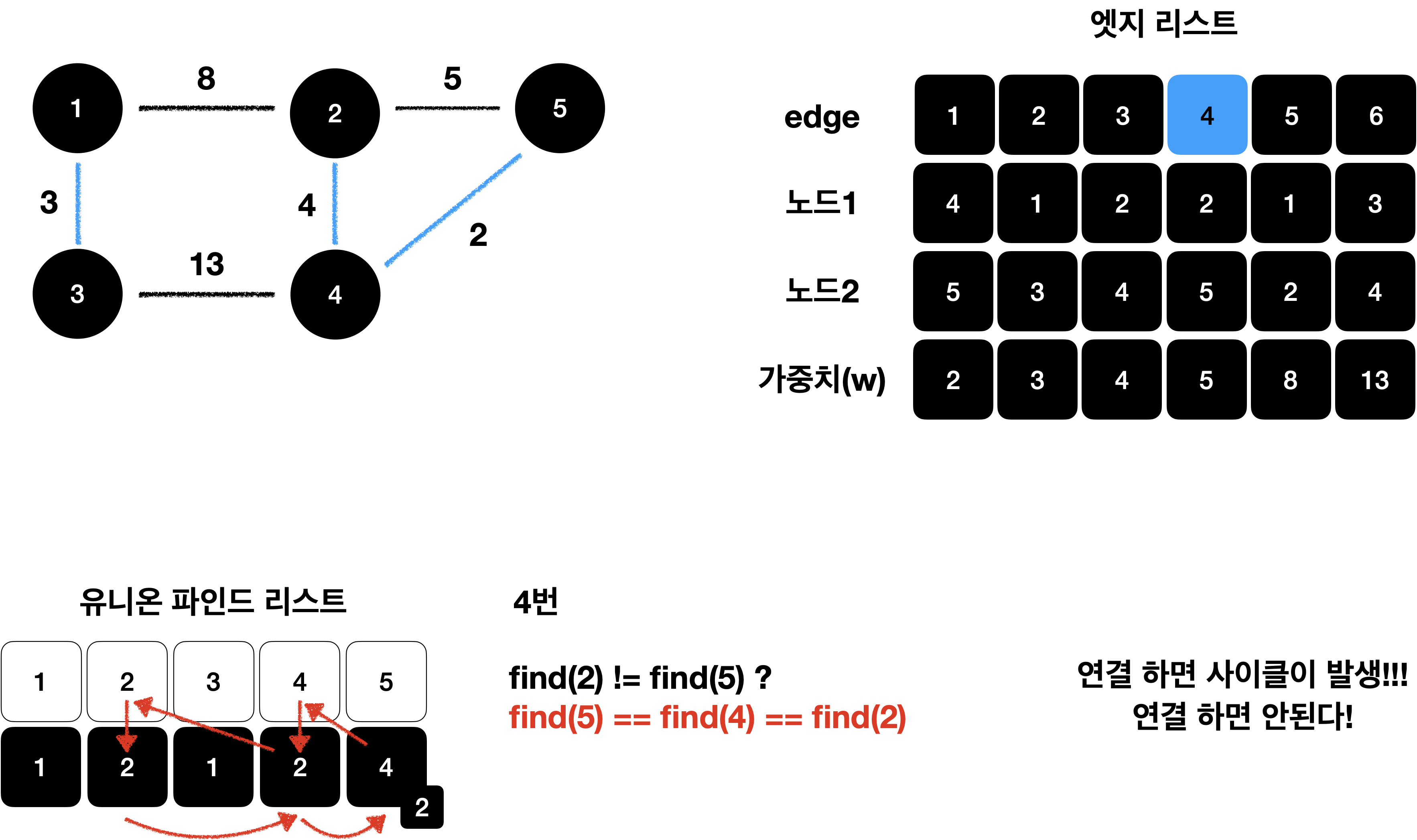
N-1번 모두 사용
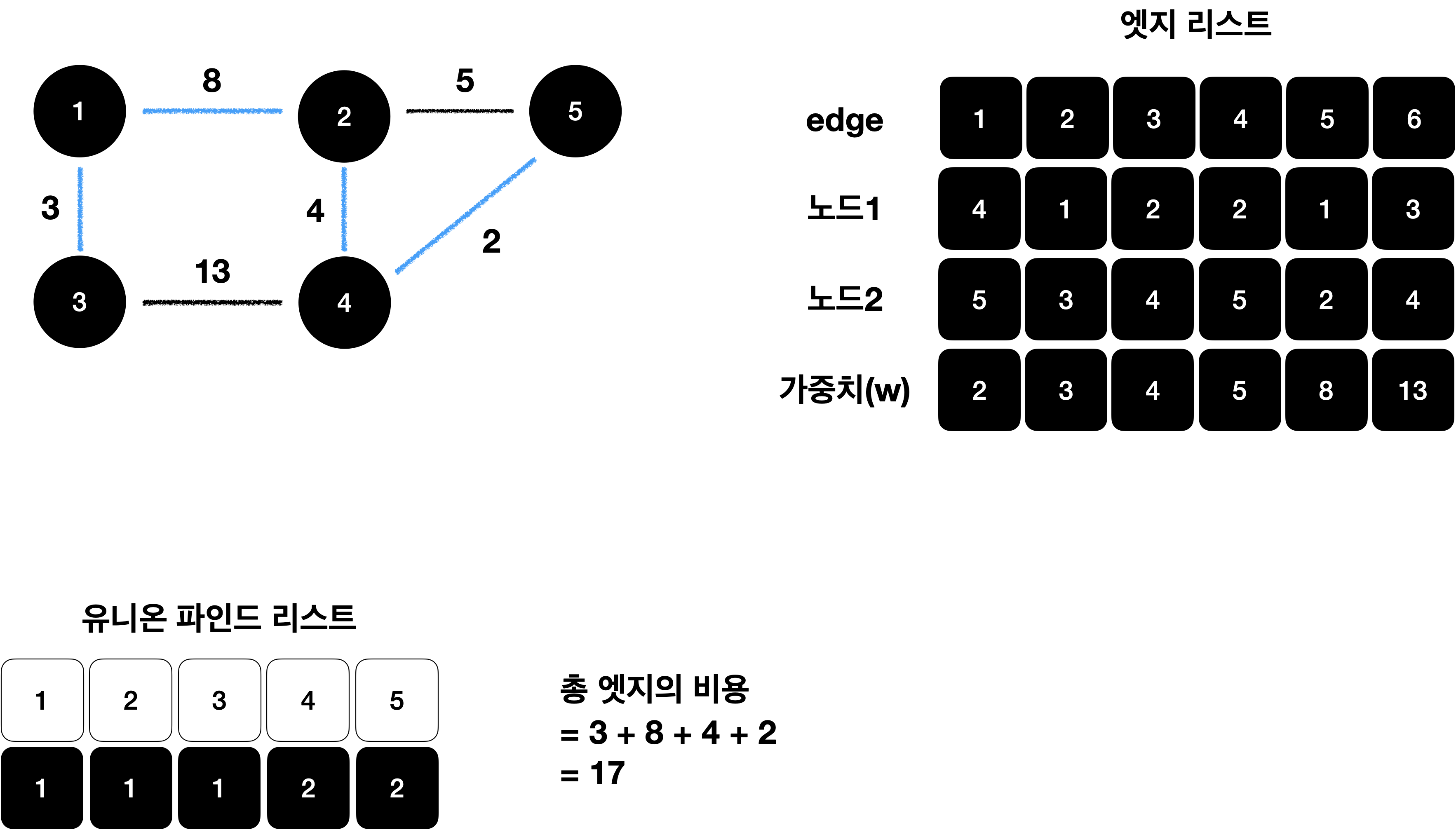
총 엣지 비용 출력
엣지의 갯수가 N-1이 되면 알고리즘을 종료하고 완성된 최소 신장 트리의 총 엣지 비용을 출력 합니다.
최소 신장 트리는 다른 그래프 알고리즘과 달리, 엣지 리스트의 형태를 이용하여 문제를 해결합니다.
엣지를 기준으로 하는 알고리즘이기 때문입니다.^^
또한, 사이클이 존재하면 안되기 때문에 이 부분은 유니온-파인드를 이용해서 처리 해야 합니다.
백준 1197
최소 신장 트리의 hello world 수준의 문제 입니다.
최소 신장 트리를 구현할 수 있으면 해결할 수 있는 문제입니다.
풀이
public class Quiz1197 {
static long sum = 0;
public static void main(String[] args) throws IOException {
/**
* 가중치가 있는 무방향 그래프에서
* 최소 비용으로 노드를 연결할 수 있는 알고리즘
* 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 정점 갯수
int v = Integer.parseInt(st.nextToken());
// 간선 갯수
int e = Integer.parseInt(st.nextToken());
// 엣지 리스트 생성
List<Node> list = new ArrayList<>();
for(int i = 0; i < e; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
list.add(new Node(start, end, weight));
}
// 가중치를 기준으로 오름차순 정렬
Collections.sort(list, Comparator.comparingInt(Node::getWeight));
// 대표노드 저장 배열 초기화
int[] parent = new int[v+1];
for(int i = 1; i <= v; i++) {
parent[i] = i;
}
int edgeCount = 0;
// 노드-1개 만큼 수행
for(int i = 0; i < e; i++) {
if(edgeCount == v - 1) break;
Node node = list.get(i);
int start = node.getStart();
int end = node.getEnd();
int weight = node.getWeight();
edgeCount += union(parent, start, end, weight);
}
System.out.print(sum);
br.close();
}
private static int union(int[] parent, int start, int end, int weight) {
// 대표노드 찾기
int ceoNode1 = find(parent, start);
int ceoNode2 = find(parent, end);
// 대표 노드가 다르면 유니온 연산 수행
if(ceoNode1 != ceoNode2) {
if(ceoNode1 > ceoNode2) {
parent[ceoNode1] = ceoNode2;
} else {
parent[ceoNode2] = ceoNode1;
}
// 최소 비용 계산
sum += weight;
return 1;
}
return 0;
}
// 대표노드 찾기
private static int find(int[] parent, int node) {
if(parent[node] == node) {
return node;
} else {
return parent[node] = find(parent, parent[node]);
}
}
private static class Node {
private int start;
private int end;
private int weight;
public Node(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getWeight() {
return weight;
}
}
}백준 1922
문제에서 컴퓨터를 연결하는 것이 방향이 없고, 연결 비용이 최소인 것을 출력하라고 했습니다.
따라서 최소 신장 트리를 사용하여 해결하면 됩니다.
최소 신장 트리는 무방향의 모든 그래프를 연결할 때 최소 비용으로 연결하는 트리 입니다.
이 점만 캐치 한다면, 최소 신장 트리의 hello world 수준의 문제 입니다.
최소 신장 트리를 구현할 수 있으면 해결할 수 있는 문제입니다.
풀이
public class Quiz1922 {
// 최소 비용
static int sum = 0;
public static void main(String[] args) throws IOException {
/**
* 최소 신장 트리?
* 무방향의 모든 그래프를 연결할 때
* 최소 비용으로 연결하는 트리
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 컴퓨터 수
int n = Integer.parseInt(br.readLine());
// 연결할 수 있는 선의 수
int m = Integer.parseInt(br.readLine());
// 엣지 리스트 생성
List<Node> edgeList = new ArrayList<>();
// 그래프로 변환
for(int i = 0; i < m; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList.add(new Node(start, end, weight));
}
// 가중치를 기준으로 오름차순 정렬
Collections.sort(edgeList, Comparator.comparingInt(Node::getWeight));
// 대표노드 생성
int[] ceoNode = new int[n+1];
for(int i = 1; i <= n; i++) {
ceoNode[i] = i;
}
int edgeCount = 0;
for(int i = 0; i < m; i++) {
// 생성 경로 = 노드 - 1개 이면 탈출
if(edgeCount == n - 1) break;
Node node = edgeList.get(i);
int start = node.getStart();
int end = node.getEnd();
int weight = node.getWeight();
edgeCount += union(ceoNode, start, end, weight);
}
System.out.print(sum);
br.close();
}
private static int union(int[] ceoNode, int start, int end, int weight) {
// 대표 노드 찾기
int ceoNode1 = find(ceoNode, start);
int ceoNode2 = find(ceoNode, end);
// 대표 노드가 다르면! 유니온 연산 수행
if(ceoNode1 != ceoNode2) {
if(ceoNode1 > ceoNode2) {
ceoNode[ceoNode1] = ceoNode2;
} else {
ceoNode[ceoNode2] = ceoNode1;
}
// 최소 비용 계산
sum += weight;
return 1;
}
return 0;
}
private static int find(int[] ceoNode, int node) {
if(ceoNode[node] == node) {
return node;
} else {
return ceoNode[node] = find(ceoNode, ceoNode[node]);
}
}
private static class Node {
private int start;
private int end;
private int weight;
public Node(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getWeight() {
return weight;
}
}
}백준 1647
혼자 해결하지 못했습니다.
하나로 연결되어 있는 마을을 분리하고 도로 유지비가 최소가 되게해야하는 부분이 어려웠습니다. ㅠㅠ
검색을 통해 해답을 보니 생각보다 엄청 쉬운 문제 였습니다.!!😊
백준1647: 도시 분할 계획 - JAVA :: 빈둥벤둥 IT logging
문제 조건
- 일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있다.
- 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다.
먼저 아래와 같은 마을이 있다고 합시다.
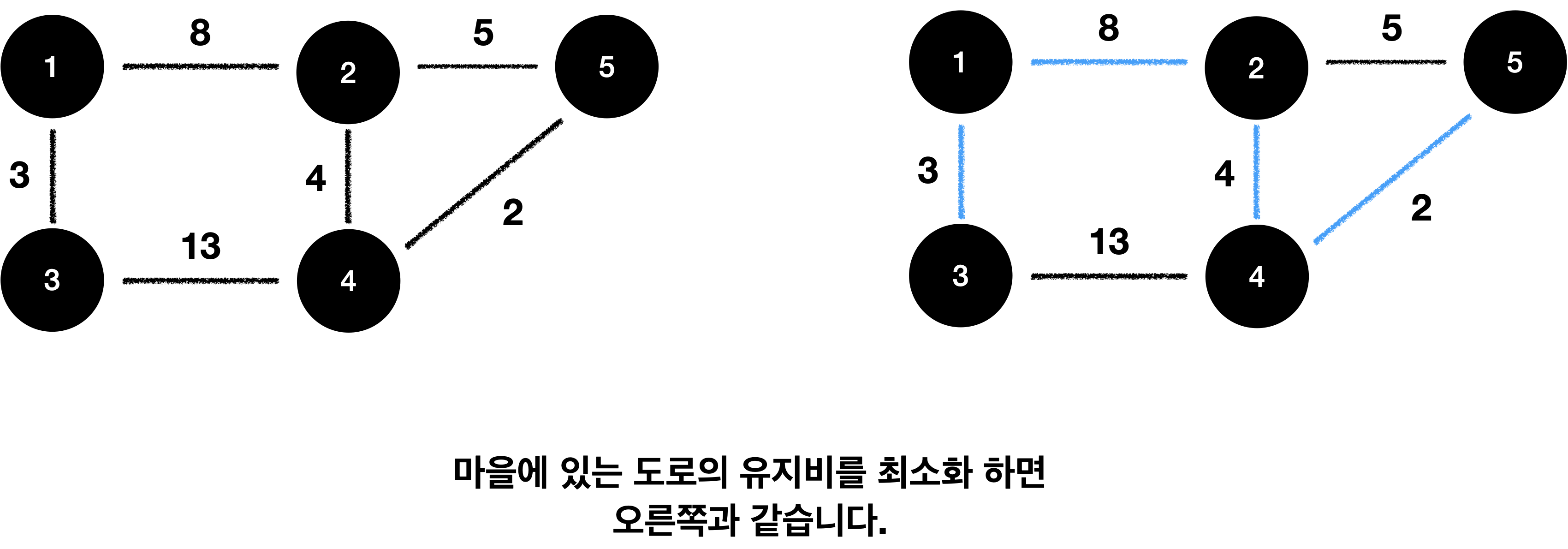
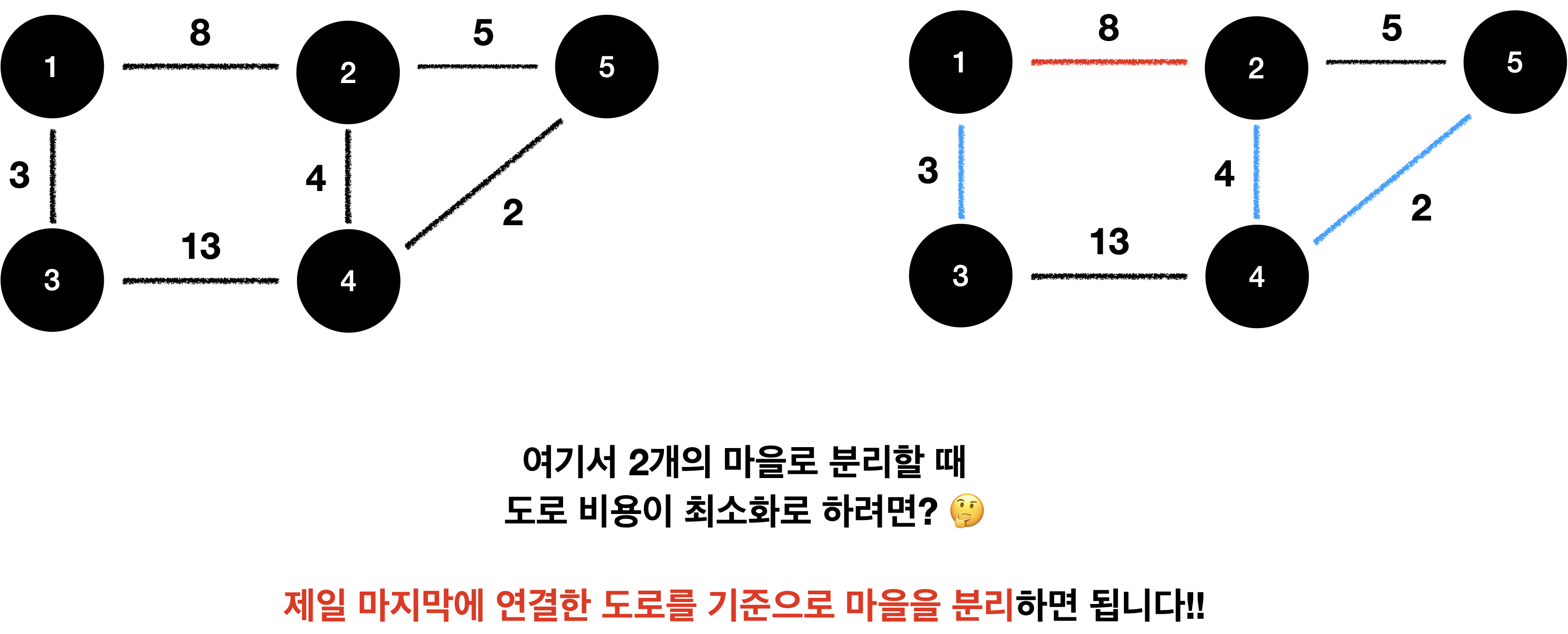
일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있습니다.!
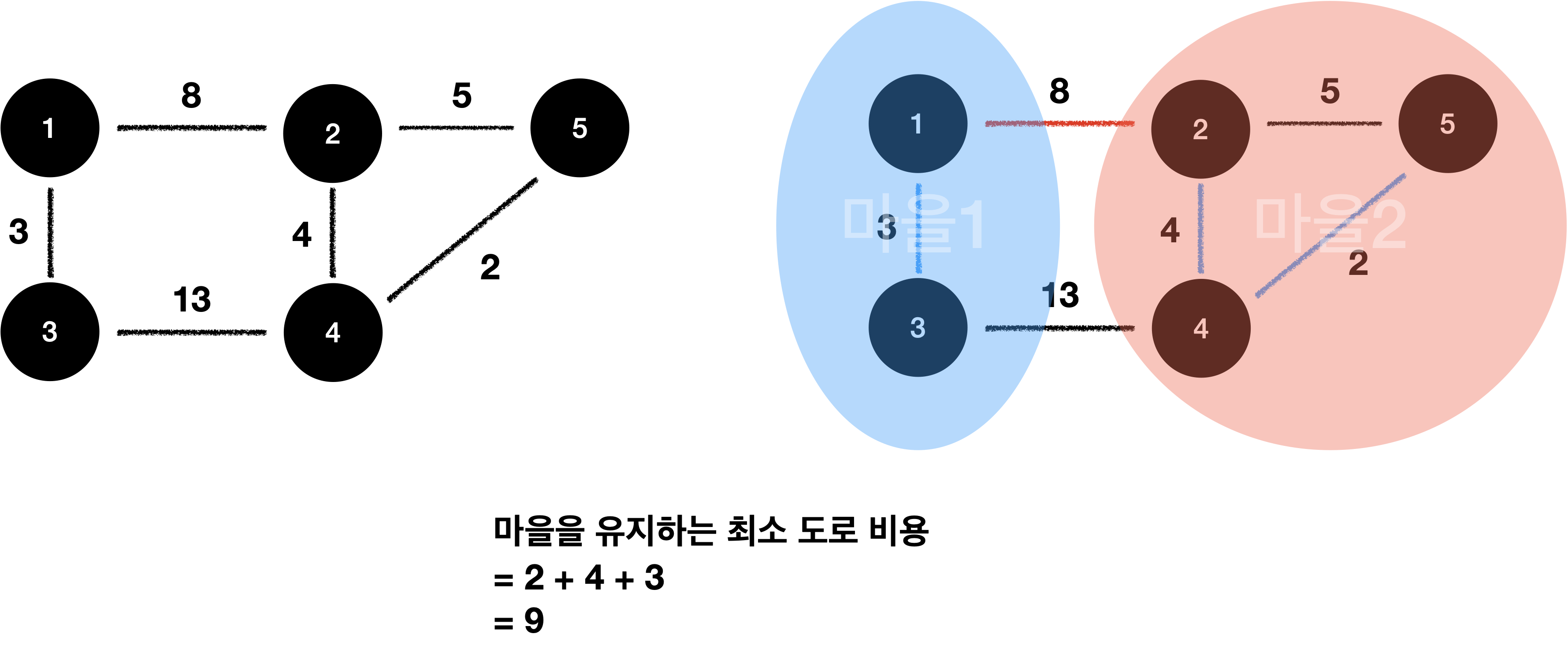
풀이
public class Quiz1674 {
// 최소 비용
static int sum = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 마을 갯수
int n = Integer.parseInt(st.nextToken());
// 도로 갯수
int m = Integer.parseInt(st.nextToken());
// 엣지 리스트 생성
List<Node> edgeList = new ArrayList<>();
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList.add(new Node(start, end, weight));
}
// 가중치를 기준으로 오름차순 정렬
Collections.sort(edgeList, Comparator.comparingInt(Node::getWeight));
// 대표노드 저장 배열
int[] ceoNode = new int[n+1];
for(int i = 1; i <= n; i++) {
ceoNode[i] = i;
}
/**
* 길의 유지비가 최소가 되도록 2개의 마을을 분리하기 위해서는
* n - 1 번째 도로를 기준으로 마을을 분리하면 된다.
*/
// 최소 비용 계산
int edgeCount = 0;
for(int i = 0; i < m; i++) {
// 필요한 도로를 완성하면 탈출
if(edgeCount == n - 2) break;
Node node = edgeList.get(i);
int start = node.getStart();
int end = node.getEnd();
int weight = node.getWeight();
edgeCount += union(ceoNode, start, end, weight);
}
System.out.print(sum);
br.close();
}
private static int union(int[] ceoNode, int start, int end, int weight) {
int ceoNode1 = find(ceoNode, start);
int ceoNode2 = find(ceoNode, end);
if(ceoNode1 != ceoNode2) {
if(ceoNode1 > ceoNode2) {
ceoNode[ceoNode1] = ceoNode2;
} else {
ceoNode[ceoNode2] = ceoNode1;
}
sum += weight;
return 1;
}
return 0;
}
private static int find(int[] ceoNode, int node) {
if(ceoNode[node] == node) {
return node;
}
return ceoNode[node] = find(ceoNode, ceoNode[node]);
}
static class Node {
private int start;
private int end;
private int weight;
public Node(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getWeight() {
return weight;
}
}
}백준 4386
- 별자리를 이루는 선은 서로 다른 두 별을 일직선으로 이은 형태이다.
- 모든 별들은 별자리 위의 선을 통해 서로 직/간접적으로 이어져 있어야 한다.
위 2가지 조건을 만족하는 별자리를 만들었을 때 최소 비용을 구하는 문제 입니다.
방향이 없는 그래프에서 경로를 만들었을 때 최소 비용을 가지면 되기 때문에 최소 신장 트리를 사용하면 됩니다.^^
문제에서 따로 시작점과 도착점을 주지 않았기 때문에
별의 위치를 기억하는 배열을 만들고
각각 별의 거리를 계산해서 엣지 리스트를 만들면 됩니다.
// 별 위치
List<Star> starPositions = new ArrayList<>();
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
double x = Double.parseDouble(st.nextToken());
double y = Double.parseDouble(st.nextToken());
starPositions.add(new Star(i, x, y));
}
// 엣지 리스트 생성
List<Star> edgeList = new ArrayList<>();
for(int i = 0; i < n; i++) {
Star star1 = starPositions.get(i);
double x1 = star1.getX();
double y1 = star1.getY();
int start = star1.getStart();
for(int j = i+1; j < n; j++) {
Star star2 = starPositions.get(j);
double x2 = star2.getX();
double y2 = star2.getY();
int end = star2.getStart();
// 거리 계산
double weight = Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));
edgeList.add(new Star(start, end, weight));
}
}
private static class Star {
private int start;
private int end;
private double x;
private double y;
private double weight;
public Star(int start, int end, double weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public Star(int start, double x, double y) {
this.start = start;
this.x = x;
this.y = y;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
public double getWeight() {
return weight;
}
}
풀이
public class Quiz4386 {
static double sum = 0f;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 별의 수
int n = Integer.parseInt(br.readLine());
// 별 위치
List<Star> starPositions = new ArrayList<>();
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
double x = Double.parseDouble(st.nextToken());
double y = Double.parseDouble(st.nextToken());
starPositions.add(new Star(i, x, y));
}
// 엣지 리스트 생성
List<Star> edgeList = new ArrayList<>();
for(int i = 0; i < n; i++) {
Star star1 = starPositions.get(i);
double x1 = star1.getX();
double y1 = star1.getY();
int start = star1.getStart();
for(int j = i+1; j < n; j++) {
Star star2 = starPositions.get(j);
double x2 = star2.getX();
double y2 = star2.getY();
int end = star2.getStart();
// 거리 계산
double weight = Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));
edgeList.add(new Star(start, end, weight));
}
}
// 가중치를 기준으로 오름차순 정렬
Collections.sort(edgeList, Comparator.comparingDouble(Star::getWeight));
// 대표 노드 저장 배열
int[] ceoNode = new int[n];
for(int i = 0; i < n; i++) {
ceoNode[i] = i;
}
int edgeCount = 0;
for(int i = 0; i < edgeList.size(); i++) {
if(edgeCount == n - 1) break;
Star star = edgeList.get(i);
int start = star.getStart();
int end = star.getEnd();
double weight = star.getWeight();
edgeCount += union(ceoNode, start, end, weight);
}
System.out.print(sum);
br.close();
}
private static int union(int[] ceoNode, int star1Node, int star2Node, double weight) {
int ceoNode1 = find(ceoNode, star1Node);
int ceoNode2 = find(ceoNode, star2Node);
if(ceoNode1 != ceoNode2) {
if(ceoNode1 > ceoNode2) {
ceoNode[ceoNode1] = ceoNode2;
} else {
ceoNode[ceoNode2] = ceoNode1;
}
sum += weight;
return 1;
}
return 0;
}
private static int find(int[] ceoNode, int node) {
if(ceoNode[node] == node) {
return node;
}
return ceoNode[node] = find(ceoNode, ceoNode[node]);
}
private static class Star {
private int start;
private int end;
private double x;
private double y;
private double weight;
public Star(int start, int end, double weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public Star(int start, double x, double y) {
this.start = start;
this.x = x;
this.y = y;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
public double getWeight() {
return weight;
}
}
}#Study/java/algorithm
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 이진 트리(백준 11725, 1911, 9934, 2263, 5639 -Java) (2) | 2023.04.12 |
|---|---|
| [알고리즘] 트리 기본 개념 (0) | 2023.04.12 |
| [알고리즘] 벨만-포드(백준 11657, 1865, 1219 -Java) (0) | 2023.04.05 |
| [알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java) (0) | 2023.04.02 |
| [알고리즘] 위상 정렬(백준 2252, 1766, 1516, 1005 -Java) (0) | 2023.04.02 |