[알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java)
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
다익스트라(Dijkstra)

방향 그래프에서 가중치가 양수일 때 출발 노드를 중심으로 최단거리를 구할 수 있는 알고리즘 입니다.
출발 노드와 모든 노드 간의 최단 거리를 탐색 합니다.
간선(엣지)는 모두 양수 이고, 시간 복잡도는 O(ElogV) 입니다.(V: 노드 수, E: 엣지 수)
특정 노드에서 다른 노드들의 최단 거리를 구하는 문제가 주어졌을 때
다익스트라 알고리즘을 사용하면 문제를 해결할 수 있습니다.
단, 그래프에서 사이클이 있으면 사용할 수 없습니다.
다익스트라 알고리즘 핵심 이론
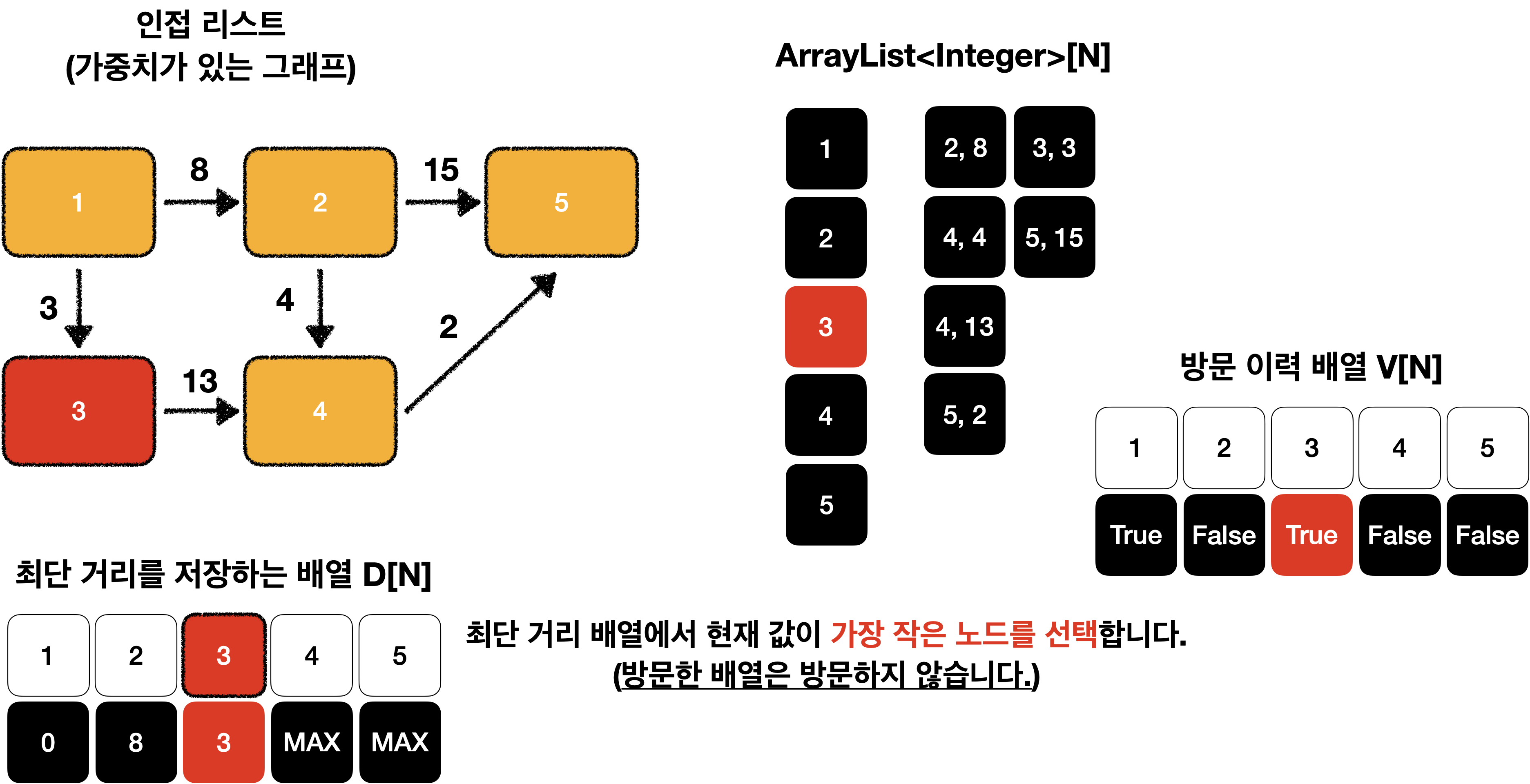
먼저 인접 리스트를 이용하여 가중치가 있는 그래프로 표현해야 합니다.
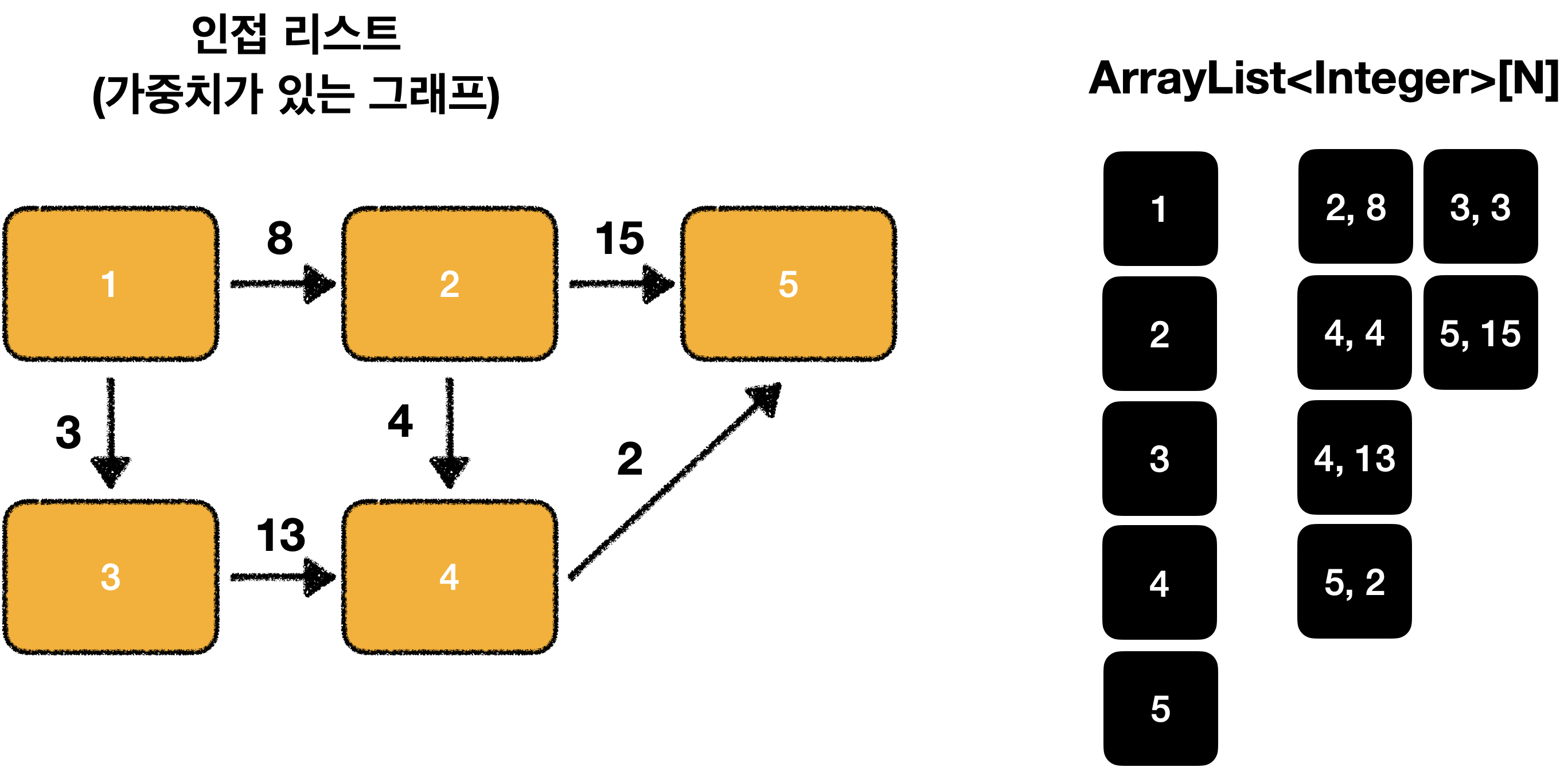
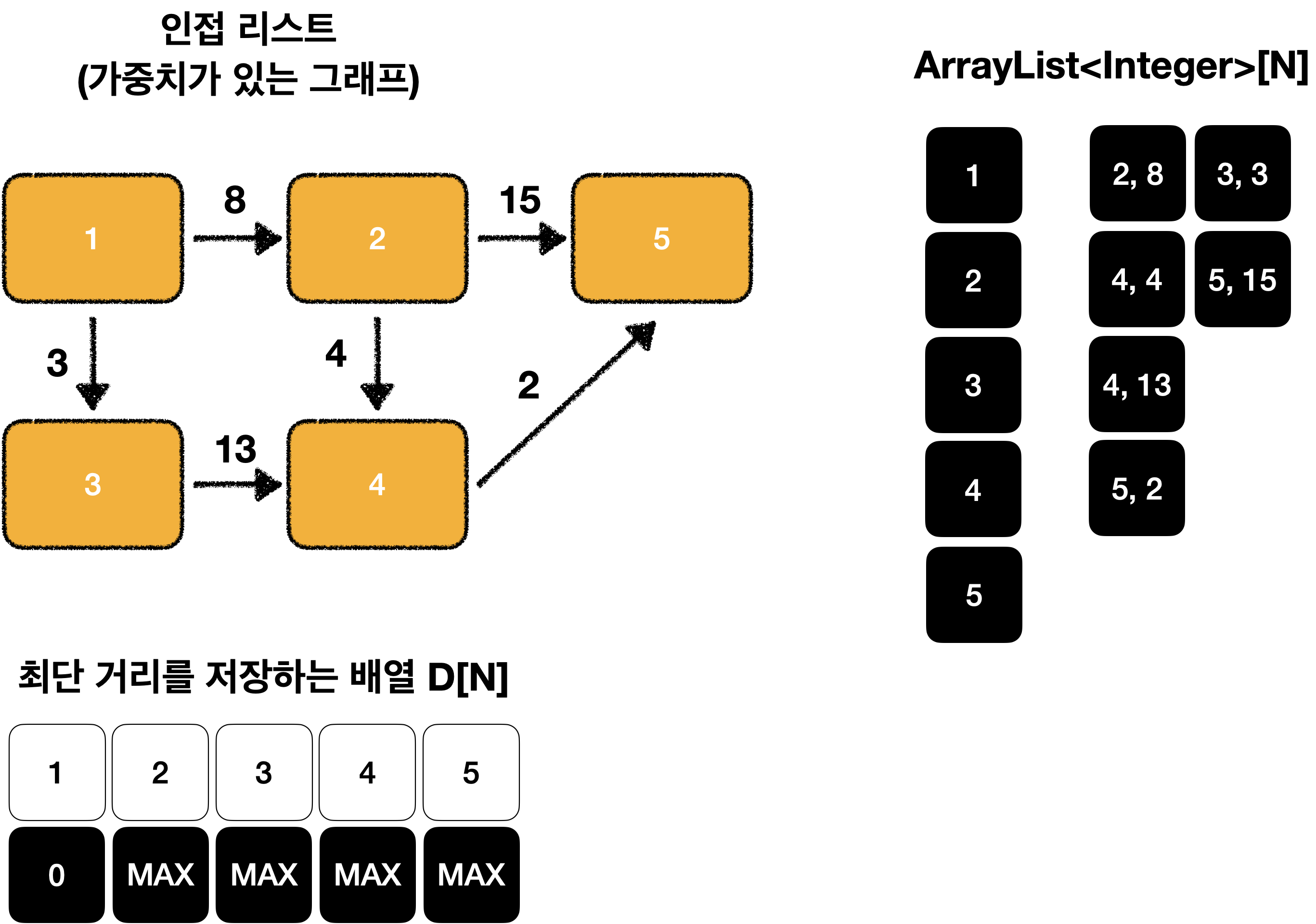
최단 거리 배열을 초기화 합니다.
최단 거리 배열을 만들고, 출발 노드의 값을 0으로, 이외의 노드는 데이터 타입의 가장 큰 값을 사용하면 됩니다.
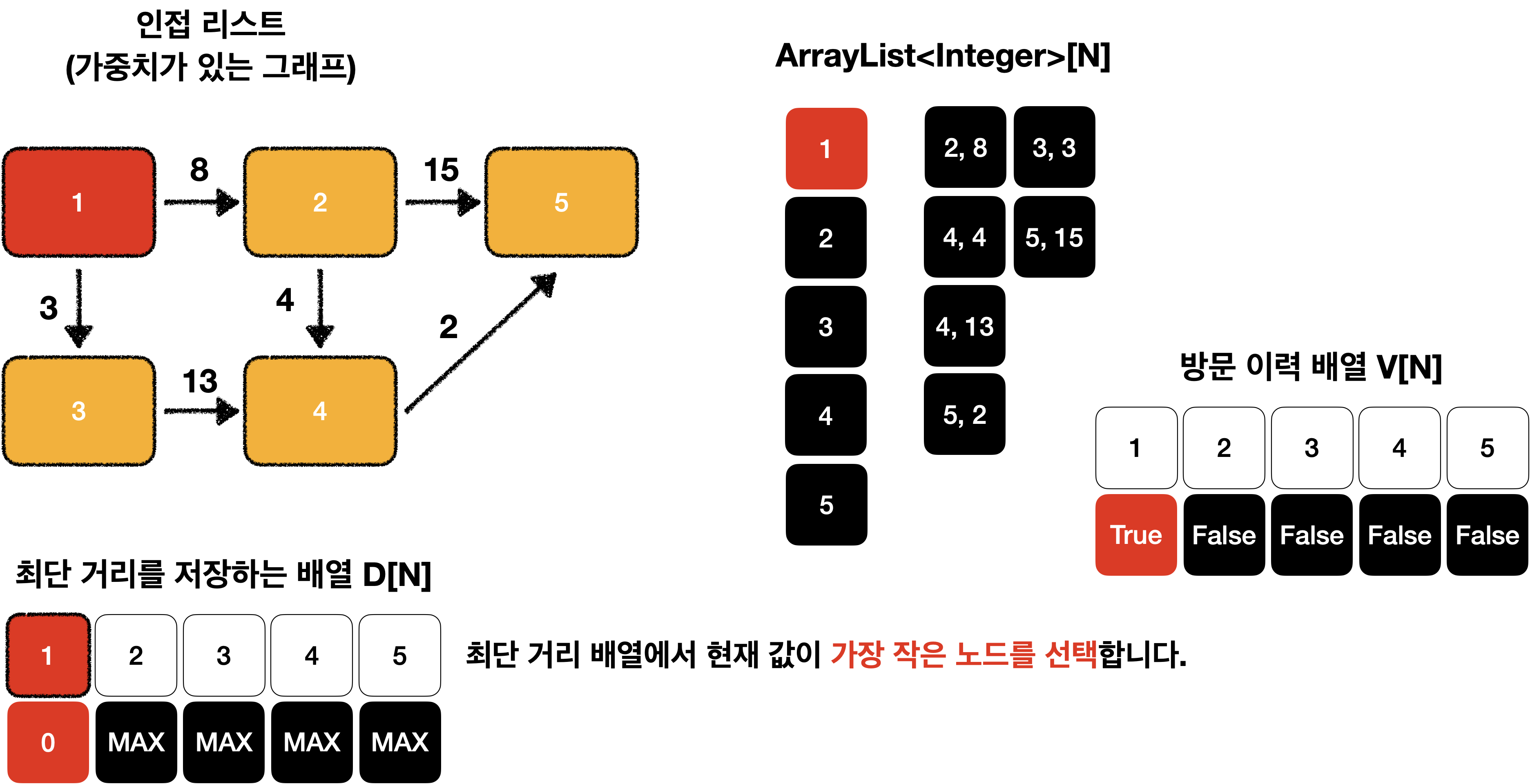
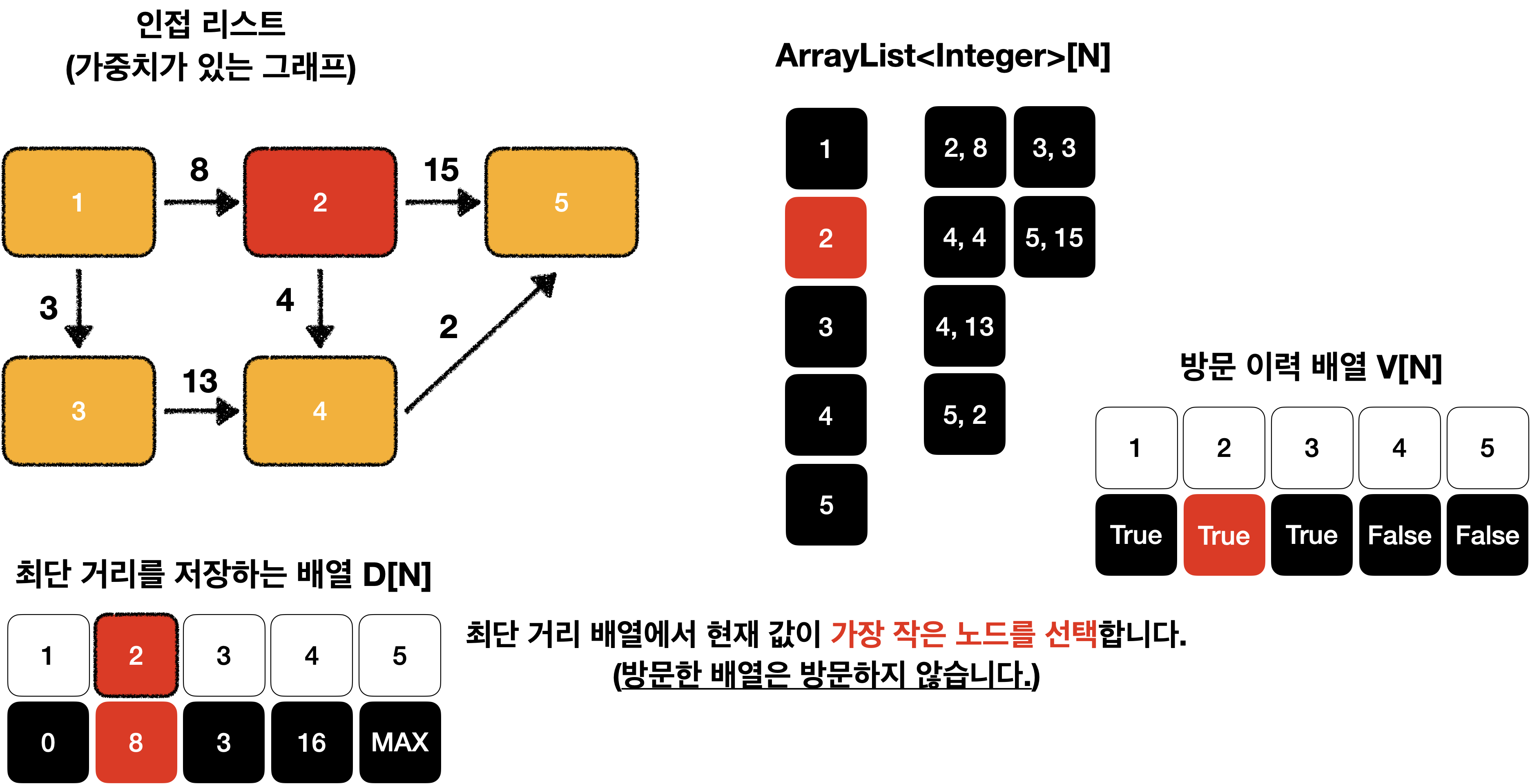
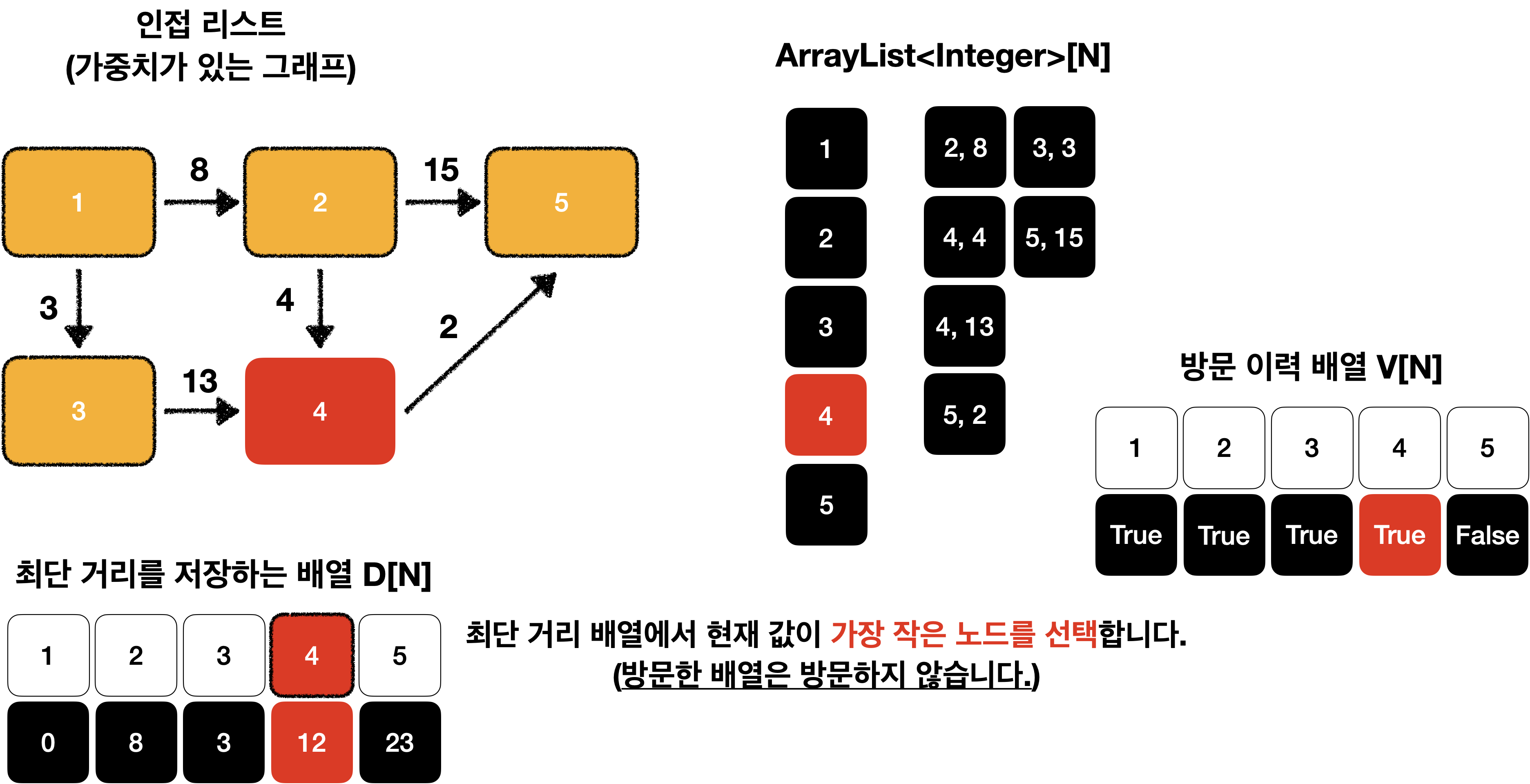
최단 거리 배열에서 현재 값이 가장 작은 노드를 선택합니다.
(여기서는 값이 0인 출발 노드에서 시작합니다.)
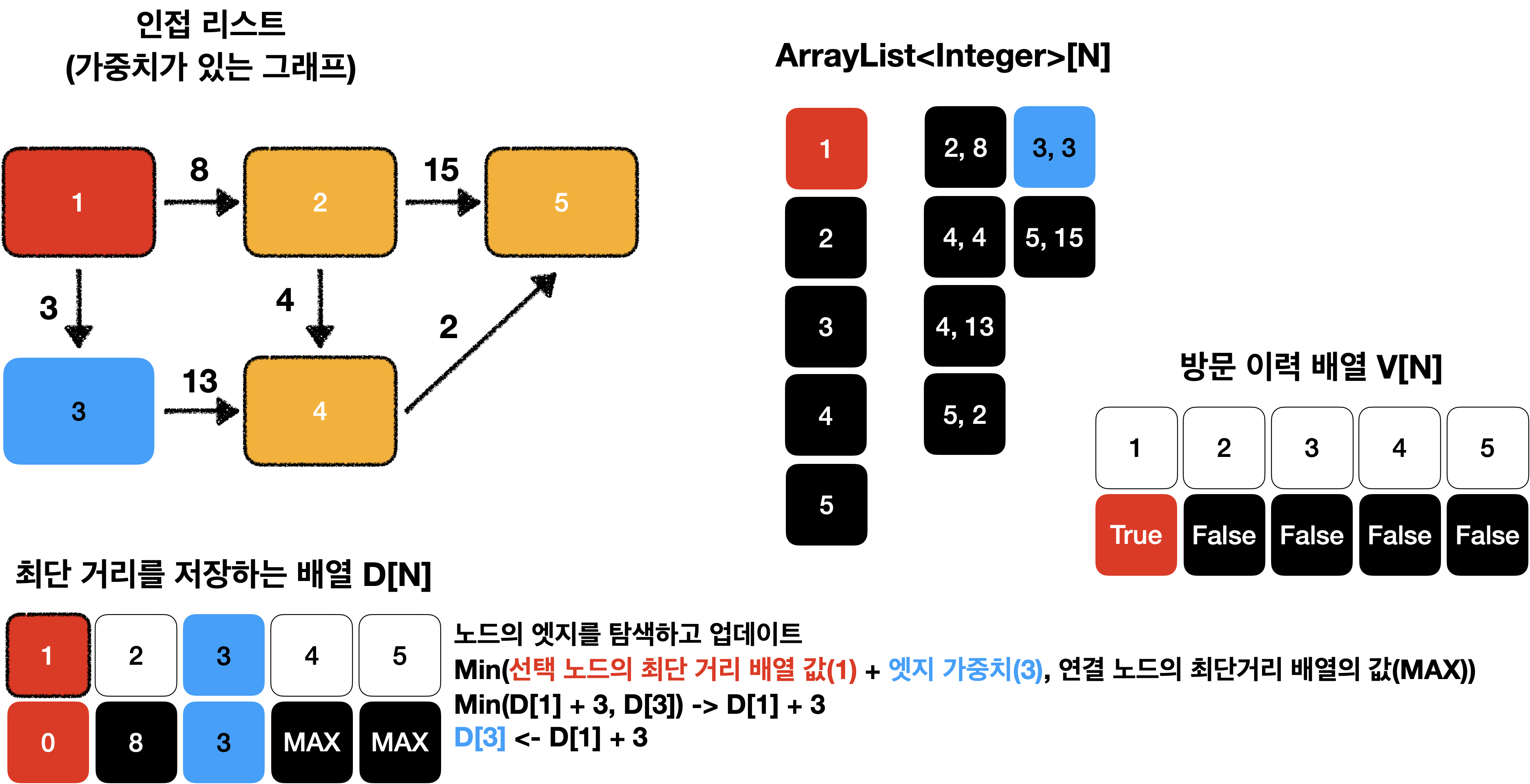
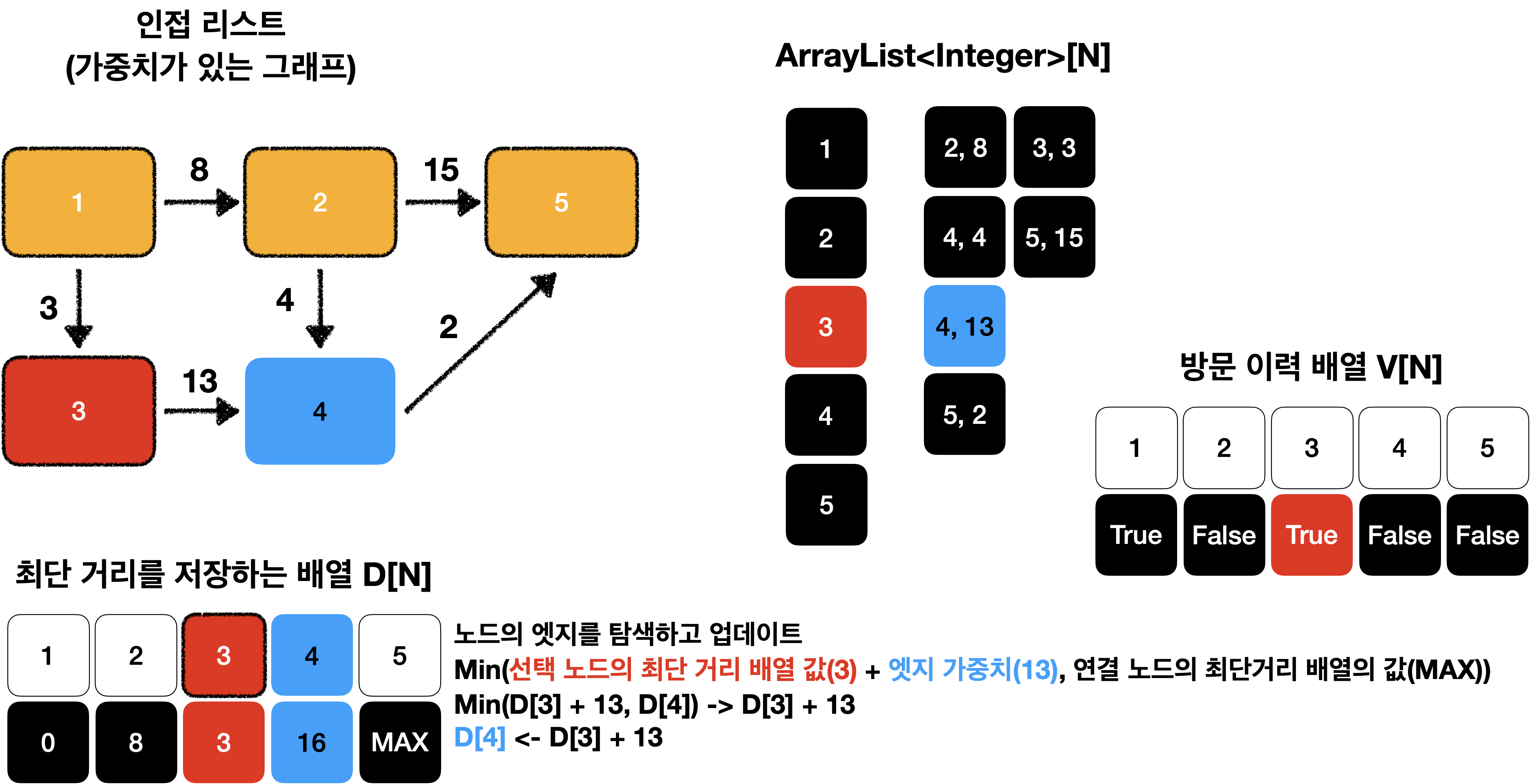
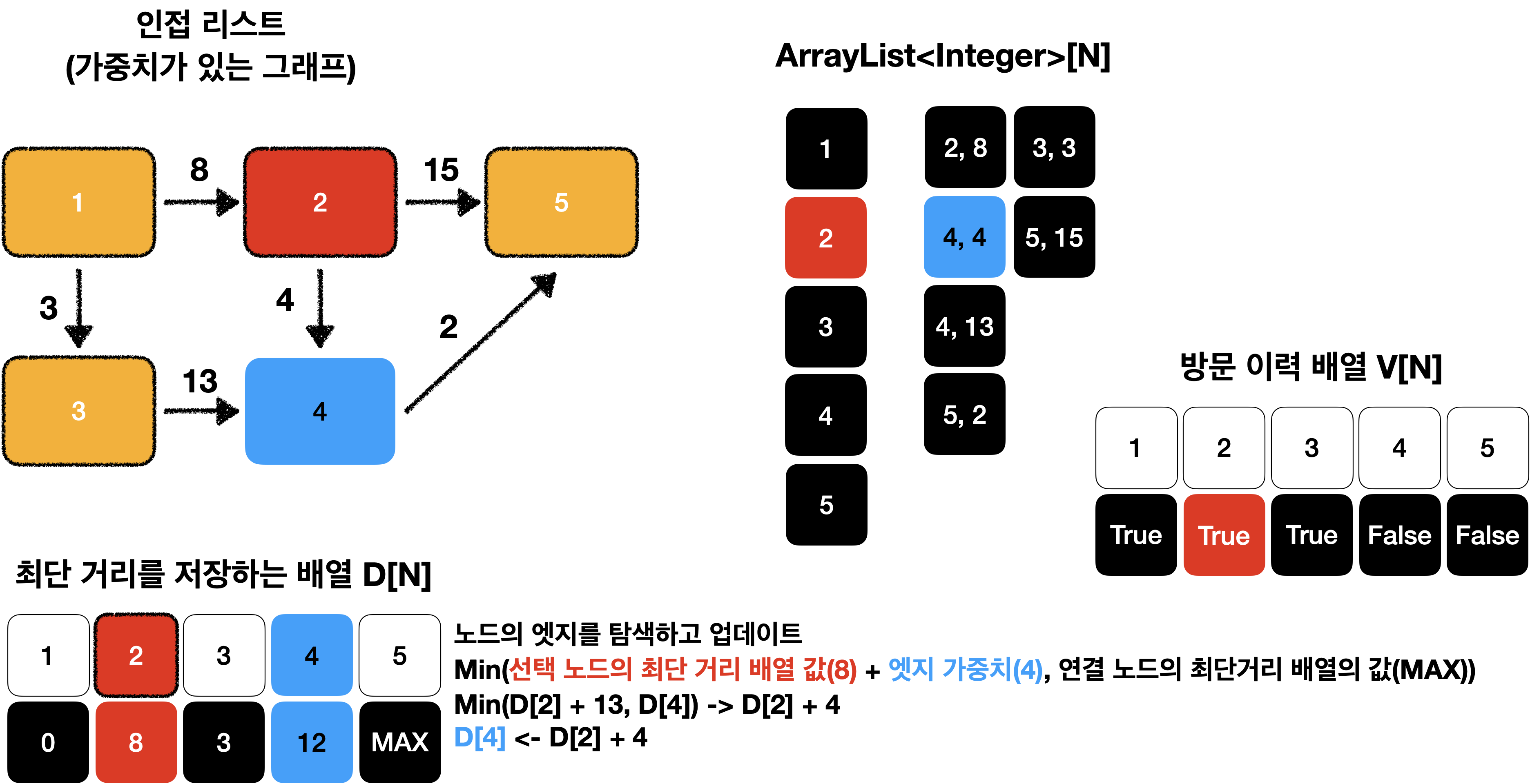
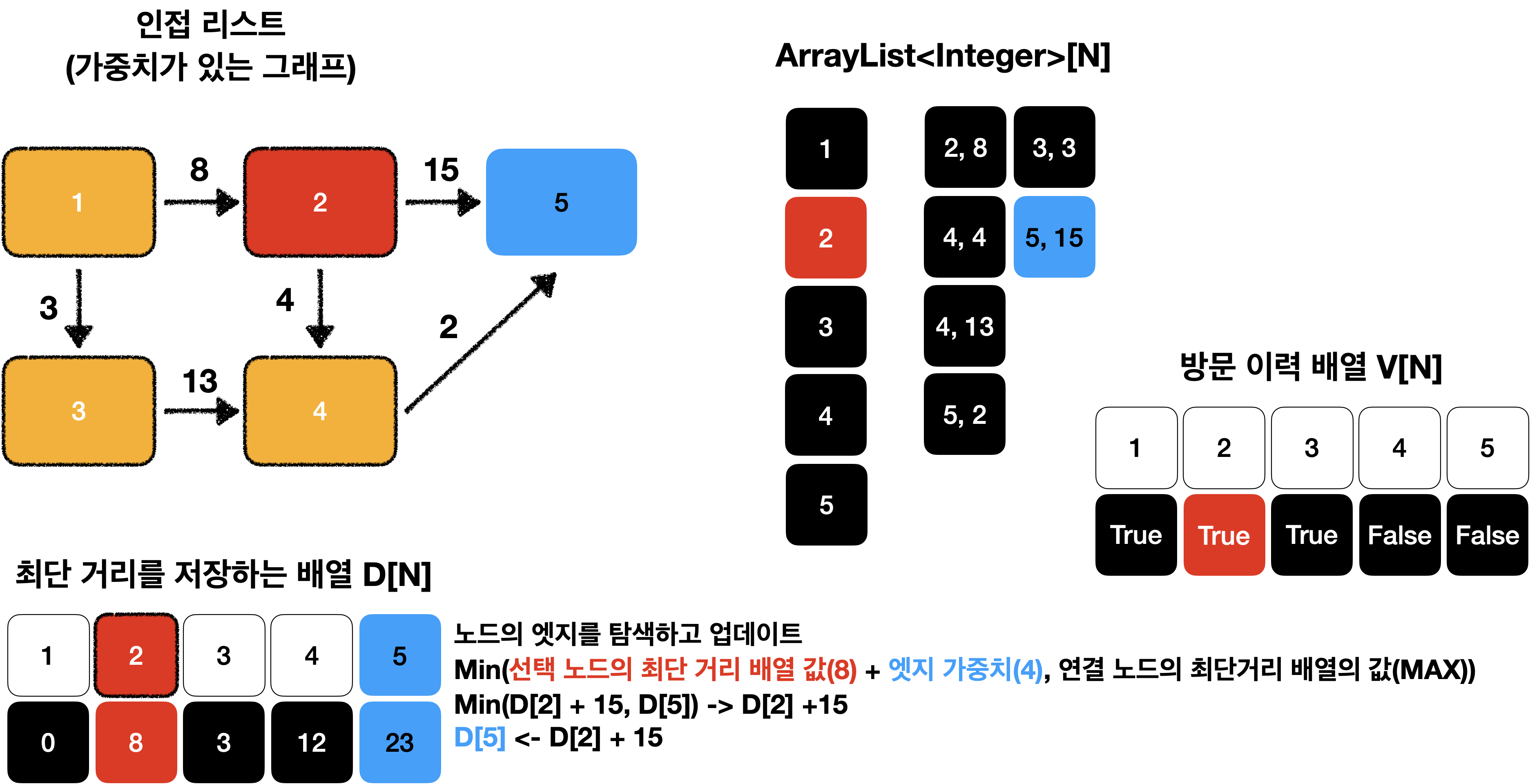
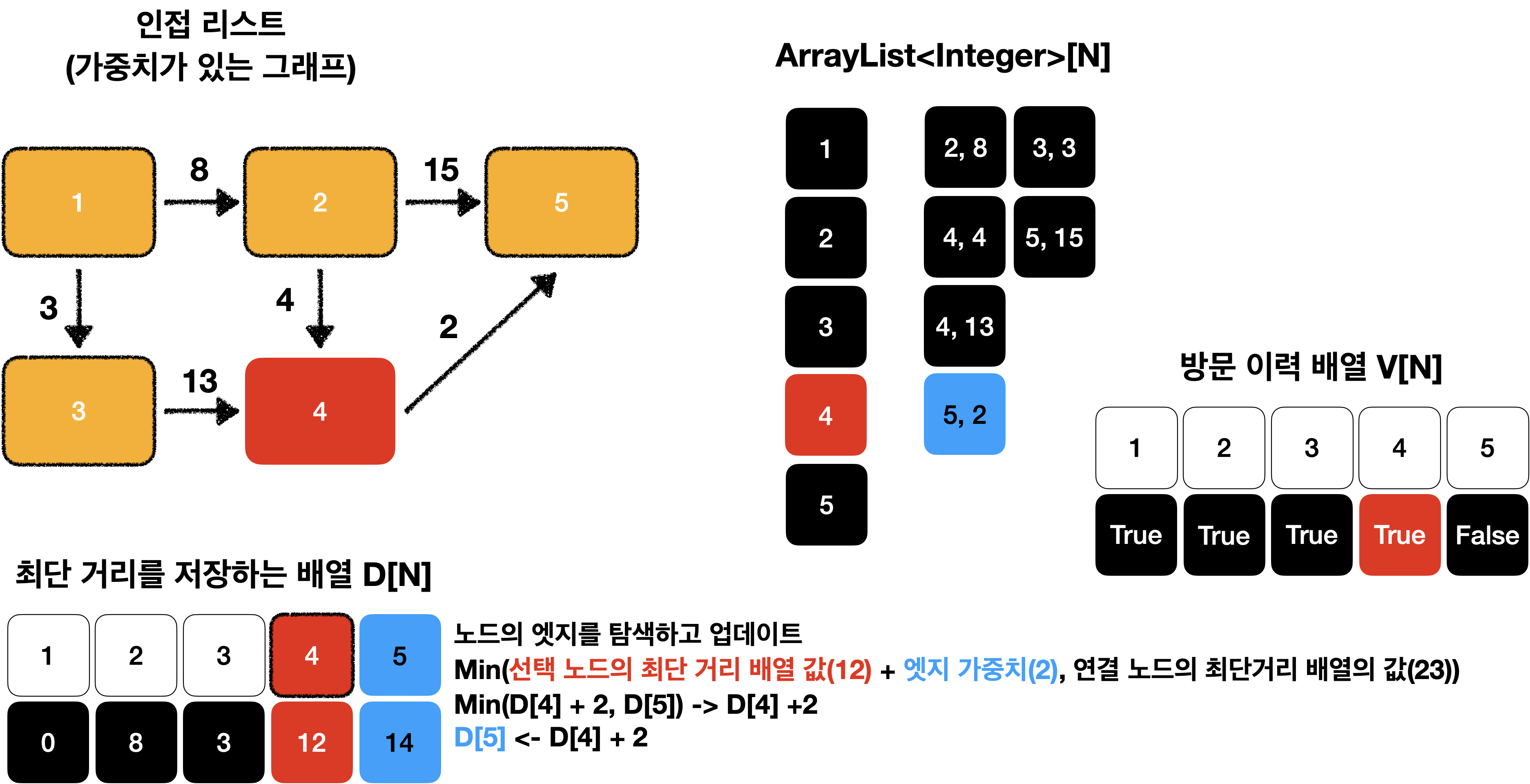
선택된 노드에 연결된 엣지의 값을 바탕으로 다른 노드의 값을 업데이트 합니다.
연결 리스트를 이용하여 현재 선택된 노드의 엣지를 탐색하고 업데이트하면 됩니다.
이때 연결 노드의 최단 거리는 아래 그림과 같이 두 값 중 더 작은 값으로 업데이트 합니다.

이 과정을 모든 노드가 처리될때 까지 반복합니다.
다시 최단 거리 배열에서 현재 값이 가장 작은 노드를 선택합니다.
(이때 노드를 다시 방문하지 않도록 방문 배열을 만들어 처리해야 합니다.)
오… 이제 더 이상 인접 노드가 없습니다!! 😭
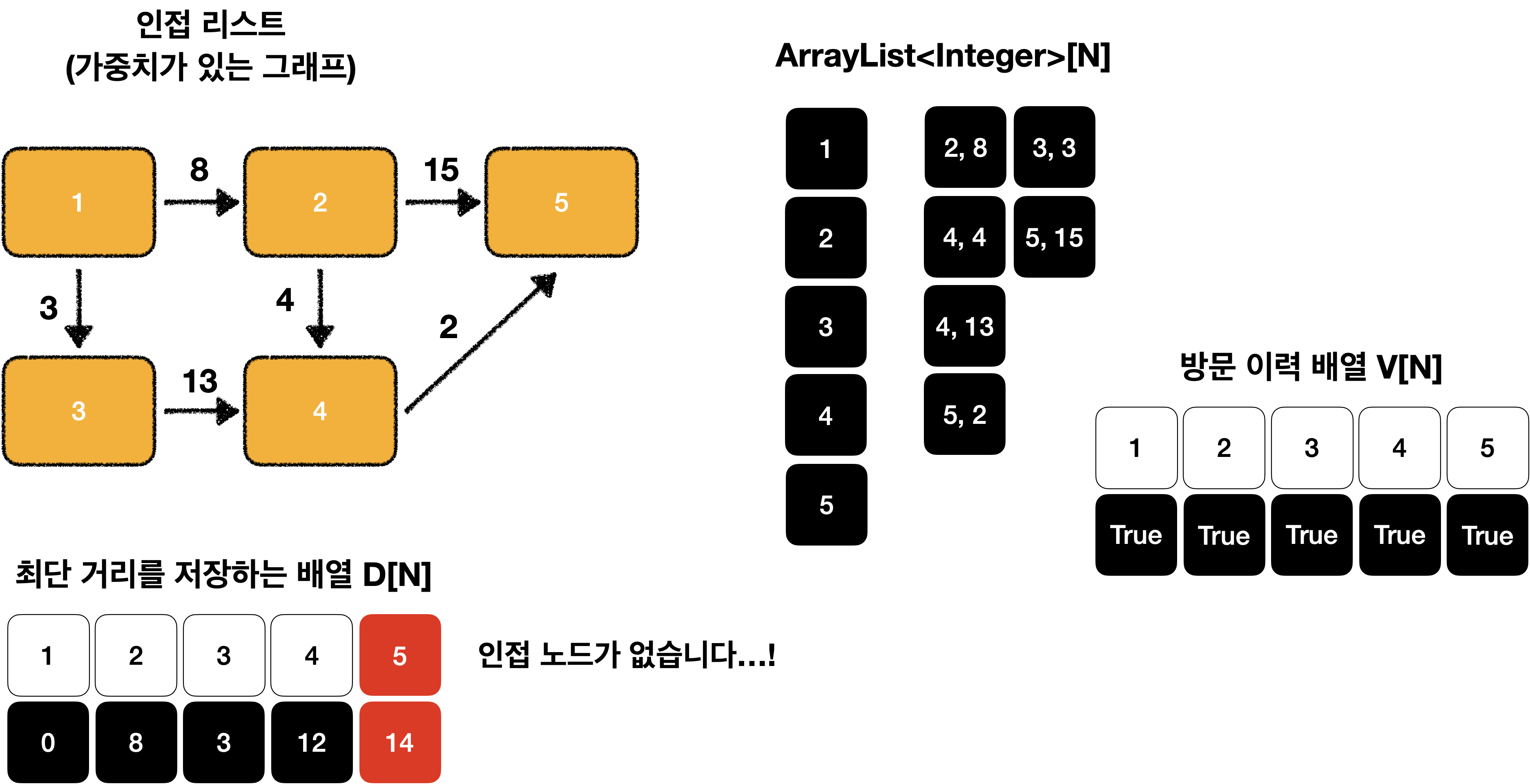
D[N]은 시작 노드 부터 i 노드 까지 최단 거리를 저장하고 있는 배열 입니다.^^

여기서는 시작노드를 1로 정했지만, 문제에 따라서 시작 노드를 정해서 D[N]을 저장하면 되겠죠?
백준 1753
1753번: 최단경로
전형적인 다익스트라 문제 입니다.
풀이
public class Quiz1753 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 정점 갯수
int v = Integer.parseInt(st.nextToken());
// 간선 갯수
int e = Integer.parseInt(st.nextToken());
// 시작 노드
int startNode = Integer.parseInt(br.readLine());
// 인접 리스트 초기화
List<Node>[] list = new ArrayList[v+1];
for(int i = 1; i <= v; i++) {
list[i] = new ArrayList<>();
}
for(int i = 0; i < e; i++) {
st = new StringTokenizer(br.readLine());
// 시작, 끝, 가중치
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 그래프로 표현
list[start].add(new Node(end, weight));
}
// 최단 거리 배열
int[] result = new int[v+1];
for(int i = 1; i <= v; i++) {
// 최단 거리를 모르기 때문에 MAX로 초기화
result[i] = Integer.MAX_VALUE;
}
// 최단 경로 계산
dijkstra(list, result, startNode, v);
StringBuilder sb = new StringBuilder();
String str = "";
for(int i = 1; i <= v; i++) {
if(result[i] == Integer.MAX_VALUE) {
str = "INF";
} else {
str = Integer.toString(result[i]);
}
sb.append(str).append("\n");
}
System.out.print(sb);
}
private static void dijkstra(List<Node>[] list, int[] result, int startNode, int v) {
// 방문 이력 배열
boolean[] visited = new boolean[v+1];
// 가중치를 기준으로 오름차순
Queue<Node> pq = new PriorityQueue<>(new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return Integer.compare(o1.getWeight(), o2.weight);
}
});
result[startNode] = 0;
pq.add(new Node(startNode, result[startNode]));
while (!pq.isEmpty()) {
Node poll = pq.poll();
if(!visited[poll.getNode()]) {
// 방문으로 처리
visited[poll.getNode()] = true;
for(Node node : list[poll.getNode()]) {
// 최단거리 계산 -> min(선택 노드의 값 + 인접 노드의 경로 가중치, 인접 노드의 값)
int min = Math.min(result[poll.getNode()] + node.getWeight(), result[node.getNode()]);
// 인접 노드의 최단거리 갱신
result[node.getNode()] = min;
// 큐에 삽입
pq.add(new Node(node.getNode(), result[node.getNode()]));
}
}
}
}
private static class Node {
private int node;
private int weight;
public Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
public int getNode() {
return node;
}
public int getWeight() {
return weight;
}
}
}백준 1238
문제에서 모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다. 라고 했습니다.
출력 값으로 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간을 요구했습니다.
따라서 학생이 X로 가는 최단경로, X에서 집으로 돌아오는 최단경로를 구해야 합니다.
풀이
public class Quiz1238 {
/**
* 각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다!!
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// n명
int n = Integer.parseInt(st.nextToken());
// m개의 도로
int m = Integer.parseInt(st.nextToken());
// x번 마을(파티 장소)
int x = Integer.parseInt(st.nextToken());
// 인접 리스트 초기화
List<Node>[] listFromX = new ArrayList[n+1];
List<Node>[] listToX = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
listFromX[i] = new ArrayList<>();
listToX[i] = new ArrayList<>();
}
// 그래프로 표현
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int time = Integer.parseInt(st.nextToken());
// x에서 오는 길
listFromX[start].add(new Node(end, time));
// x로 가는 길
listToX[end].add(new Node(start, time));
}
// X에서 다른 정점까지 최단 거리 저장 배열
int[] distanceFromX = new int[n+1];
// 다른 정점에서 X까지 최단 거리 저장 배열
int[] distanceToX = new int[n+1];
for(int i = 1; i <=n; i++) {
distanceFromX[i] = Integer.MAX_VALUE;
distanceToX[i] = Integer.MAX_VALUE;
}
// x에서 각 노드의 최단거리 distance
// 각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다.
int[] dijkstara1 = dijkstara(listToX, distanceToX, m, x);
int[] dijkstara2 = dijkstara(listFromX, distanceFromX, m, x);
int max = Integer.MIN_VALUE;
for(int i = 1; i <= n; i++) {
max = Math.max(max, dijkstara1[i] + dijkstara2[i]);
}
System.out.print(max);
br.close();
}
public static int[] dijkstara(List<Node>[] list, int[] distance, int n, int x) {
// 최단거리 == 최소시간, 최단거리를 기준으로 내림차순
Queue<Node> priorityQueue = new PriorityQueue<>(new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return Integer.compare(o1.getTime(), o2.getTime());
}
});
// 노드 방문 이력
boolean[] visited = new boolean[n+1];
distance[x] = 0;
priorityQueue.offer(new Node(x, distance[x]));
while (!priorityQueue.isEmpty()) {
Node node = priorityQueue.poll();
if(!visited[node.getNode()]) {
// 방문 완료
visited[node.getNode()] = true;
// 선택 노드의 인접 노드 탐색
for(Node nd : list[node.getNode()]) {
// 선택 노드의 최단 거리 배열 값 + 엣지 가중치, 연결 노드의 최단거리 배열의 값
int min = Math.min(distance[node.getNode()] + nd.getTime(), distance[nd.getNode()]);
distance[nd.getNode()] = min;
priorityQueue.add(new Node(nd.getNode(), distance[nd.getNode()]));
}
}
}
return distance;
}
static class Node {
private int node;
private int time;
public Node(int node, int time) {
this.node = node;
this.time = time;
}
public int getNode() {
return node;
}
public int getTime() {
return time;
}
}
}백준 1916
다익스트라 알고리즘을 구현하면 해결할 수 있는 문제 입니다.
풀이
public class Quiz1916 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 도시 갯수
int n = Integer.parseInt(br.readLine());
// 버스 갯수
int m = Integer.parseInt(br.readLine());
// 인접 리스트 초기화
List<Bus>[] list = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
for(int i = 0; i < m; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
// 출발 도시 번호
int start = Integer.parseInt(st.nextToken());
// 도착 도시 번호
int end = Integer.parseInt(st.nextToken());
// 버스 비용
int paid = Integer.parseInt(st.nextToken());
// 그래프 생성
list[start].add(new Bus(end, paid));
}
StringTokenizer st = new StringTokenizer(br.readLine());
// 출발 도시
int startCity = Integer.parseInt(st.nextToken());
// 도착 도시
int endCity = Integer.parseInt(st.nextToken());
// 최단 거리 배열
int[] result = new int[n+1];
for(int i = 1; i <= n; i++) {
// 최단 거리를 모르기 때문에 최대로 저장
result[i] = Integer.MAX_VALUE;
}
// 최단 경로 계산
int[] dijkstra = dijkstra(list, result, n, startCity);
System.out.print(dijkstra[endCity]);
br.close();
}
private static int[] dijkstra(List<Bus>[] list, int[] result, int n, int startCity) {
// 비용을 기준으로 오름차순
Queue<Bus> pq = new PriorityQueue<>(new Comparator<Bus>() {
@Override
public int compare(Bus o1, Bus o2) {
return Integer.compare(o1.getPaid(), o2.getPaid());
}
});
// 방문 이력 배열
boolean[] visited = new boolean[n+1];
// 출발
result[startCity] = 0;
pq.add(new Bus(startCity, result[startCity]));
while (!pq.isEmpty()) {
Bus poll = pq.poll();
// 방문하지 않으면
if(!visited[poll.getNum()]) {
// 방문!
visited[poll.getNum()] = true;
for(Bus bus : list[poll.getNum()]) {
// 최단 거리 계산 -> min(선택 노드의 최단거리 + 인접 노드의 가중치, 인접 노드의 최단거리)
int min = Math.min(result[poll.getNum()] + bus.getPaid(), result[bus.getNum()]);
// 최단 거리 저장
result[bus.getNum()] = min;
// 큐에 삽입
pq.add(new Bus(bus.getNum(), result[bus.getNum()]));
}
}
}
return result;
}
private static class Bus {
private int num;
private int paid;
public Bus(int num, int paid) {
this.num = num;
this.paid = paid;
}
public int getNum() {
return num;
}
public int getPaid() {
return paid;
}
}
}백준 4485
2차원 인접 리스트를 만들어서 다익스트라 알고리즘을 사용하여 해결하면 됩니다.
// 인접 리스트
List<Node>[][] list = new ArrayList[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
list[i][j] = new ArrayList<>();
}
}
풀이
public class Quiz4485 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int count = 0;
while (true) {
// 동굴 크기
int n = Integer.parseInt(br.readLine());
// 동굴의 크기가 0이면 종료
if(n == 0) break;
// 인접 리스트
List<Node>[][] list = new ArrayList[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
list[i][j] = new ArrayList<>();
}
}
// 동굴, 인접 리스트 생성
int[][] map = new int[n][n];
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 0; j < n; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
list[i][j].add(new Node(i, j, map[i][j]));
}
}
int startX = 0;
int startY = 0;
// 최단 거리 저장 배열
int[][] result = new int[n][n];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// 쵀댓값으로 초기화
result[i][j] = Integer.MAX_VALUE;
}
}
// 최소비용 탐색
dijkstra(list, map, result, startX, startY, n);
count++;
sb.append("Problem ")
.append(count)
.append(": ")
.append(result[n-1][n-1])
.append("\n");
}
System.out.print(sb);
br.close();
}
private static void dijkstra(List<Node>[][] list, int[][] map, int[][] result, int startX, int startY, int n) {
Queue<Node> pq = new PriorityQueue<>(
(o1, o2) -> Integer.compare(o1.getWeight(), o2.getWeight())
);
// 방문 이력
boolean[][] visited = new boolean[n][n];
visited[startX][startY] = true;
// 최단 거리
result[startX][startY] = map[startX][startY];
pq.add(new Node(startX, startY, result[startX][startY]));
while (!pq.isEmpty()) {
Node poll = pq.poll();
int[] ud = {1, -1, 0, 0};
int[] lr = {0, 0, 1, -1};
for(int i = 0; i < 4; i++) {
int newX = poll.getX() + ud[i];
int newY = poll.getY() + lr[i];
if(newX < 0 || newY < 0 || newX >= n || newY >= n) continue;
if (!visited[newX][newY]) {
// 방문 등록
visited[newX][newY] = true;
for (Node nodes : list[newX][newY]) {
// 최소 비용 계산
int min = Math.min(result[poll.getX()][poll.getY()] + nodes.getWeight(), result[nodes.getX()][nodes.getY()]);
// 최소 비용 저장
result[nodes.getX()][nodes.getY()] = min;
// 큐에 삽입
pq.add(new Node(nodes.getX(), nodes.getY(), result[nodes.getX()][nodes.getY()]));
}
}
}
}
}
private static class Node {
private int x;
private int y;
private int weight;
public Node(int x, int y, int weight) {
this.x = x;
this.y = y;
this.weight = weight;
}
public int getX() {
return x;
}
public int getY() {
return y;
}
public int getWeight() {
return weight;
}
}
}
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386 -Java) (0) | 2023.04.10 |
|---|---|
| [알고리즘] 벨만-포드(백준 11657, 1865, 1219 -Java) (0) | 2023.04.05 |
| [알고리즘] 위상 정렬(백준 2252, 1766, 1516, 1005 -Java) (0) | 2023.04.02 |
| [알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java) (0) | 2023.03.29 |
| [알고리즘] 이분 그래프(백준 1707, 1953, 12893 -Java) (0) | 2023.03.25 |