[알고리즘] 벨만-포드(백준 11657, 1865, 1219 -Java)
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
벨만-포드

벨만-포드 알고리즘은 방향 그래프에서 가중치가 양수/음수일 때 출발 노드를 중심으로 최단거리를 구할 수 있는 알고리즘 입니다.
특정 출발 노드에서 다른 모든 노드까지의 최단 거리를 구하는 알고리즘!!!
(벨만-포드 알고리즘은 출발점이 특정한 점일때 사용 가능한 알고리즘)
엇…! 🤔 다익스트라 알고리즘도 방향 그래프에서 최단 거리를 구하는 알고리즘 인데요.
자세한 내용은 이 포스팅을 확인해 주세요!!
알고리즘 다익스트라(백준 1238, 1753, 1916, 4485 -Java)
[알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java)
[알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java) 알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇 본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
howisitgo1ng.tistory.com
다익스트라는 가중치가 양수인 경우에만 사용이 가능하지만,
벨만-포드는 가중치가 음수인 경우에도 최단 거리를 구할 수 있는 알고리즘 입니다!
추가로, 전체 그래프에서 음수 사이클이 존재하는지 파악할 수 있는 알고리즘 입니다.
시간 복잡도는 O(VE) 입니다.
참고
유니온 파인드 알고리즘은 무방향 그래프의 사이클 유무를 판단할 수 있습니다.^^find(노드1) == find(노드2) 이면 사이클이 발생한 것 입니다.
알고리즘 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java)
[알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java)
[알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040) 알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇 본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니
howisitgo1ng.tistory.com
벨만-포드 핵심 이론
✅엣지 리스트로 그래프를 구현하고 최단 경로 리스트 초기화 하기
벨만-포드는 엣지를 중심으로 동작하기 때문에, 그래프를 엣지 리스트로 구현 합니다.
최단 경로 리스트를 출발 노드는 0, 나머지 노드는 무한으로 초기화 합니다.
출발 노드가 1일 때를 예로 설명 하겠습니다.^^
이를 그림으로 표현하면 다음과 같습니다.

✅모든 엣지를 확인하여 정답 리스트 업데이트
최단 거리 배열에서 업데이트 반복 횟수는 노드 갯수 - 1 입니다.
노드 갯수가 N이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 엣지의 최대 갯수는 N - 1 이기 때문 입니다.
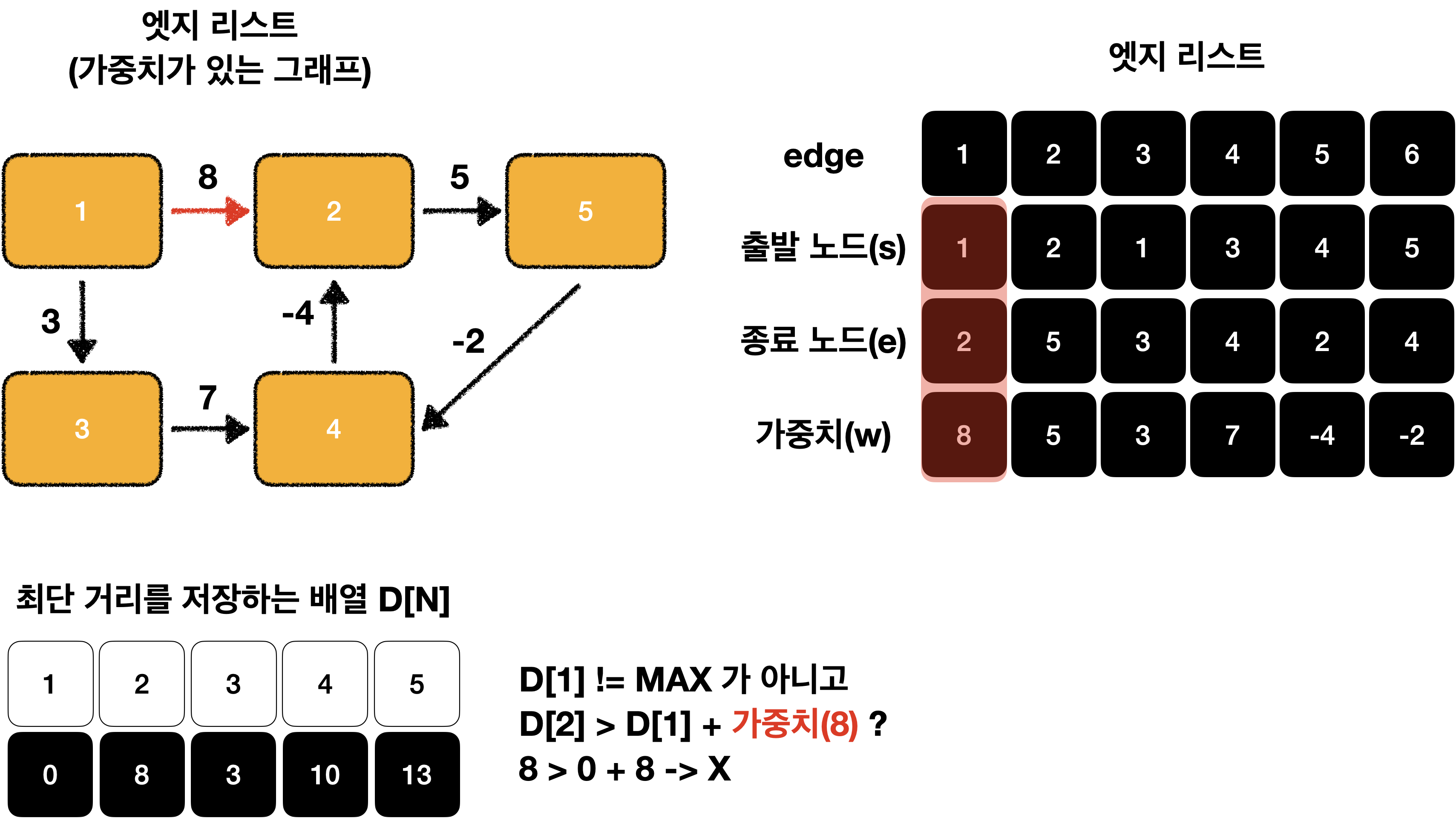
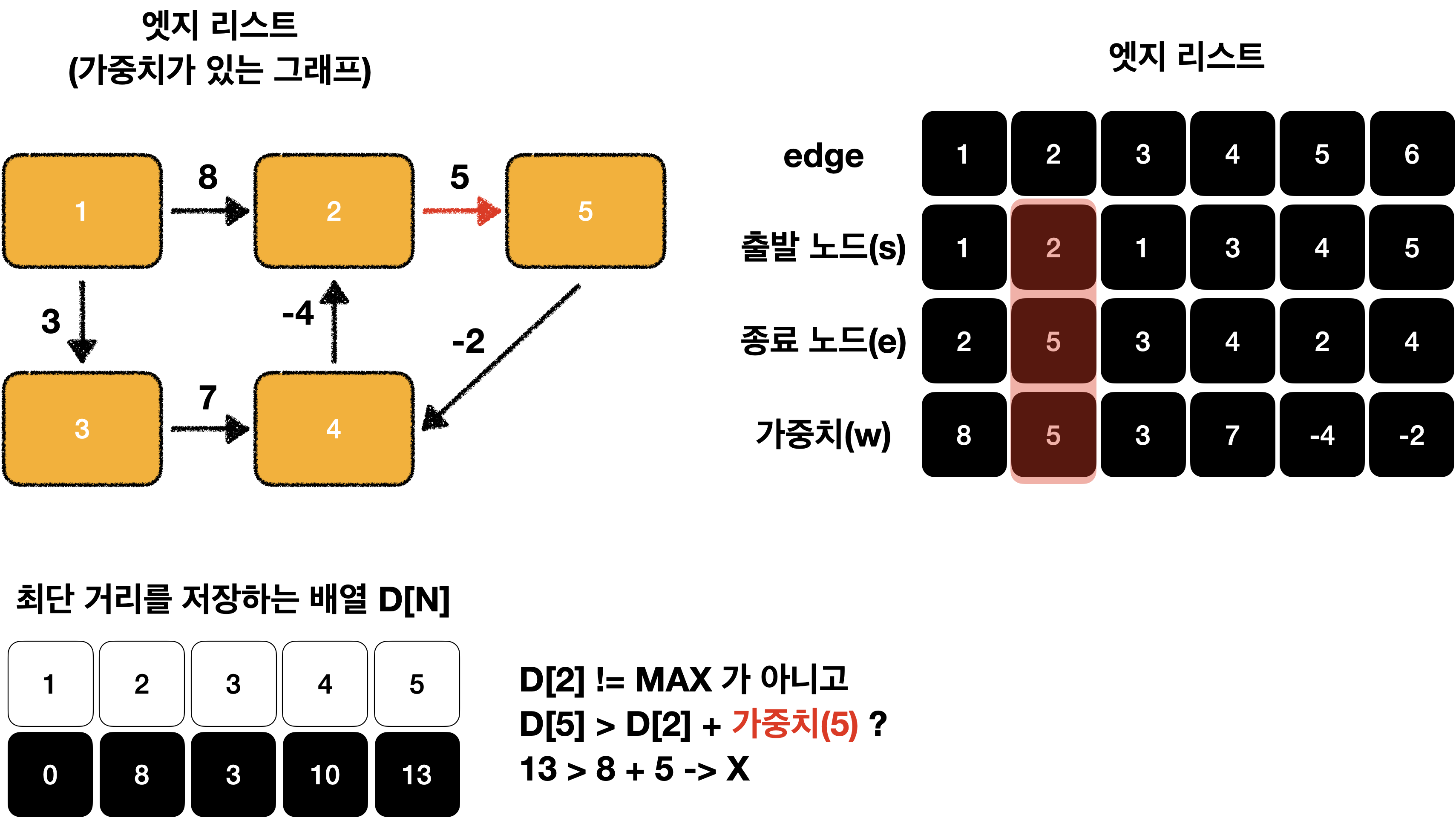
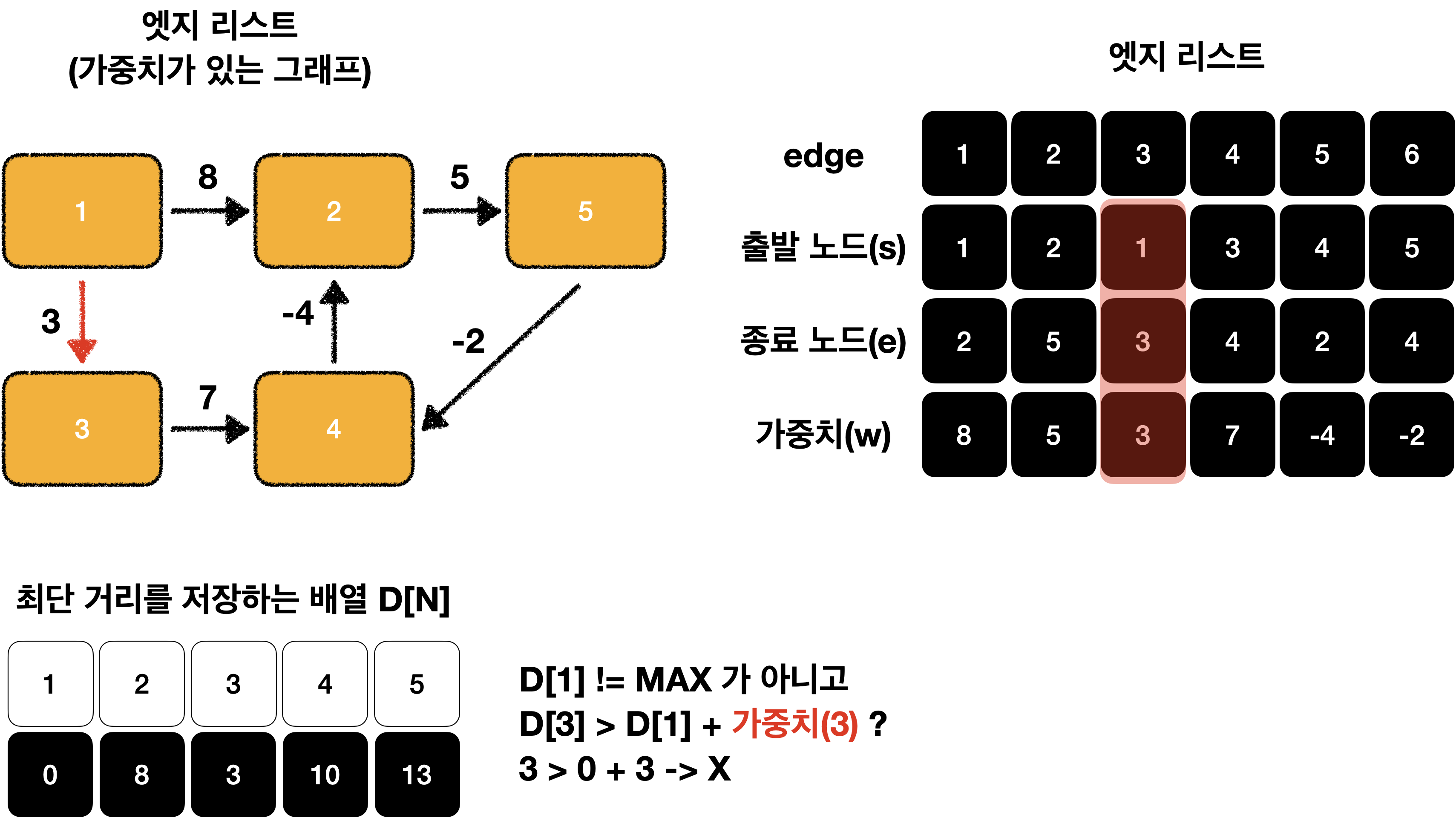
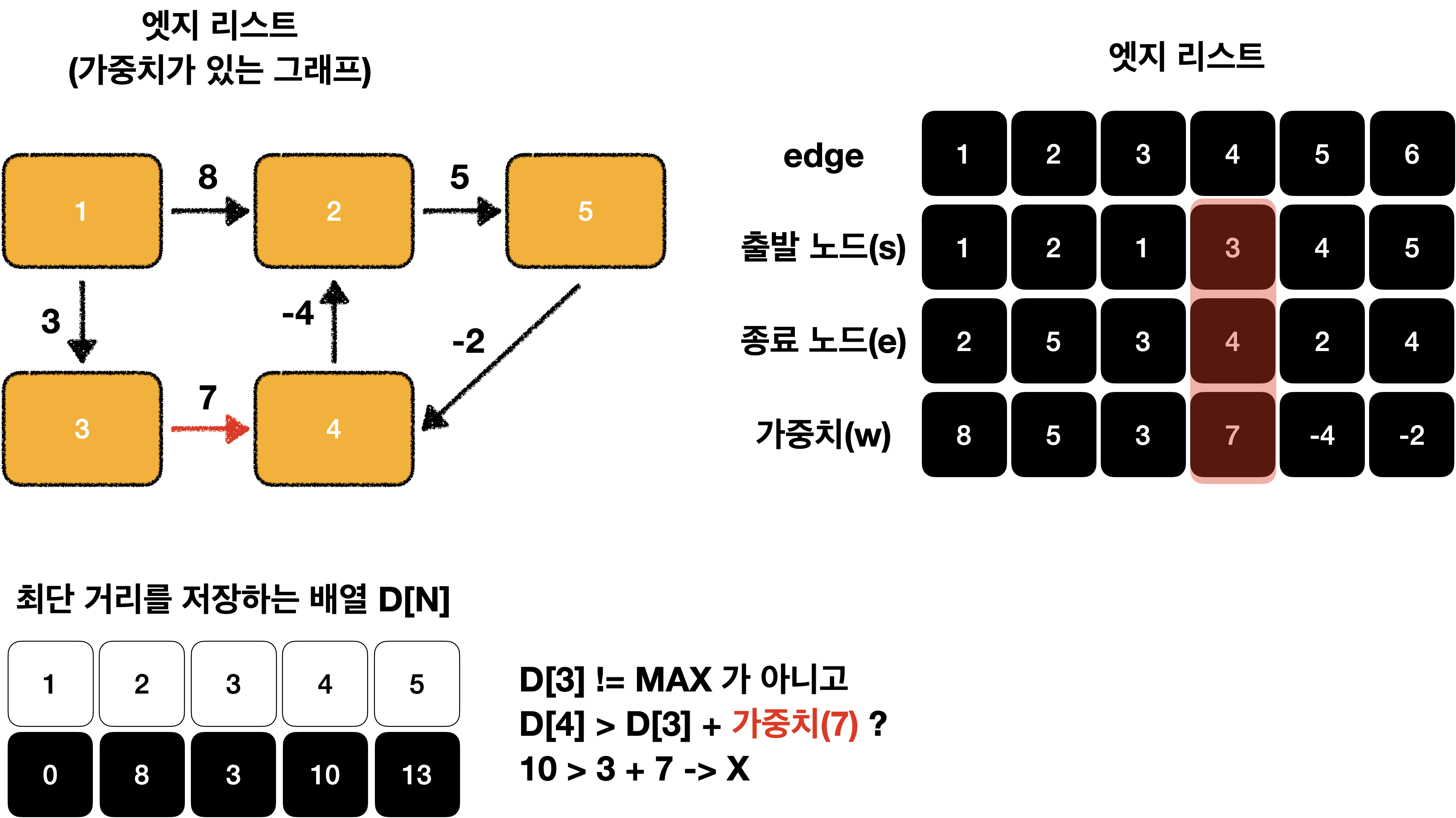
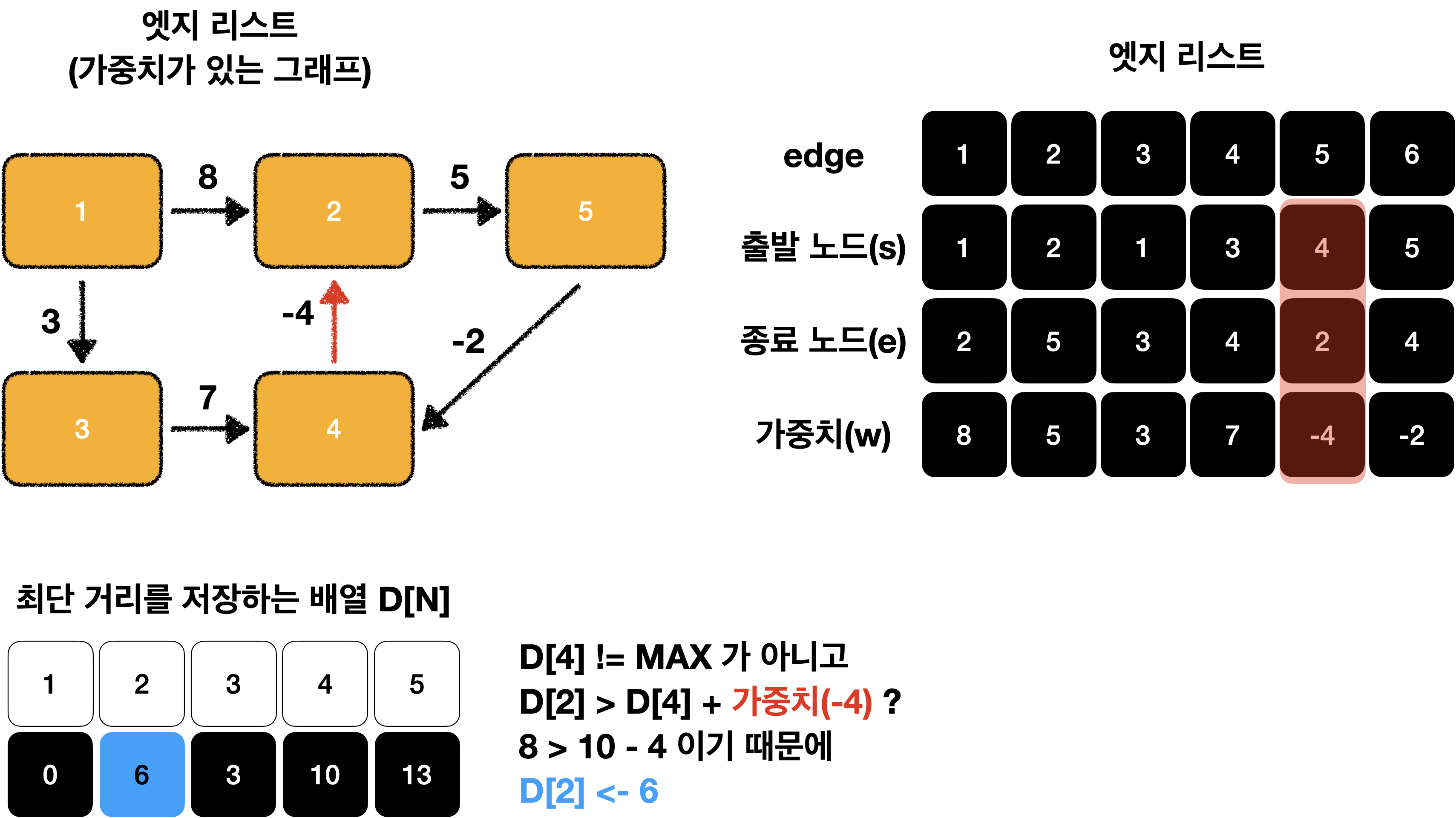
모든 엣지 E = (s, e, w)에서 다음 조건을 만족하면 업데이트를 실행 합니다.
업데이트 반복 횟수가 K번 이라면
해당 시점에 최단 거리를 저장하는 배열의 값은 시작점에서 K개의 엣지를 사용했을 때 각 노드에 대한 최단 거리 입니다.
D[s] != MAX 이고 D[e] > D[s] + w 일 때 D[e] = D[s] + w로 리스트의 값을 업데이트 합니다.
if(D[s] != MAX && D[e] > D[s] + w) {
D[e] = D[s] + w;
}먼저 노드 1에서 엣지 1개를 사용했을 때를 구해보겠습니다.
이를 그림으로 표현하면 다음과 같습니다.
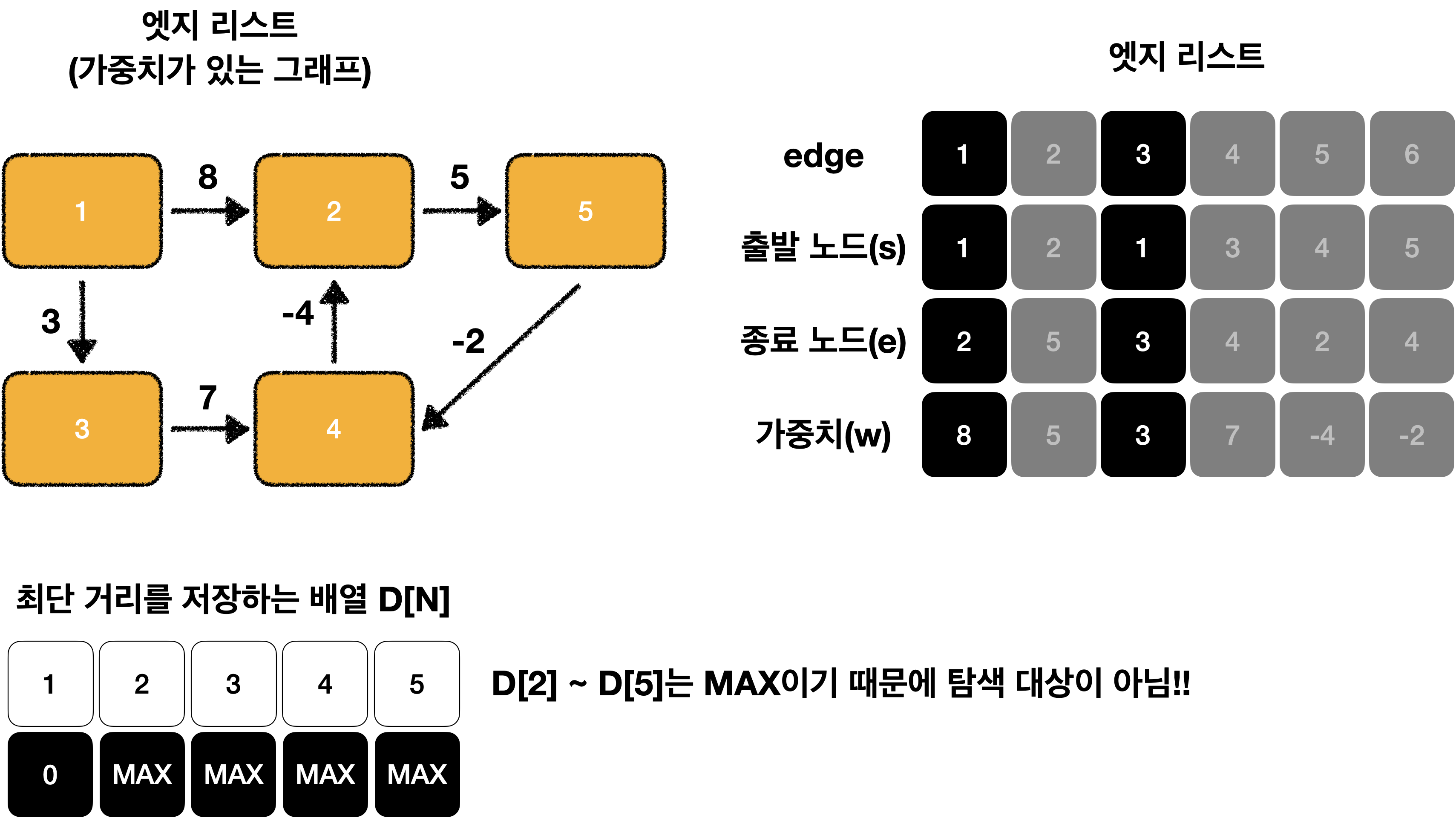
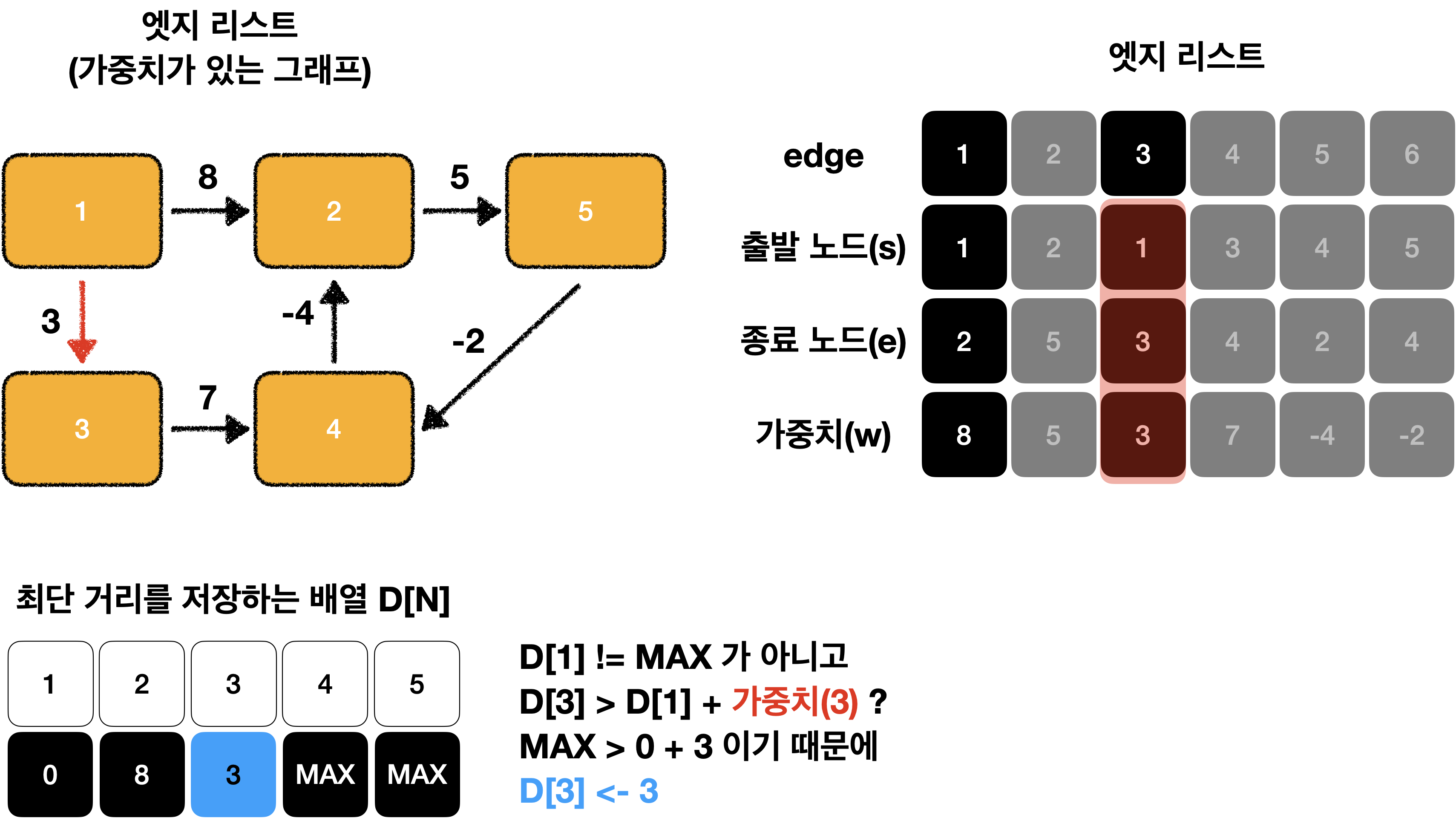
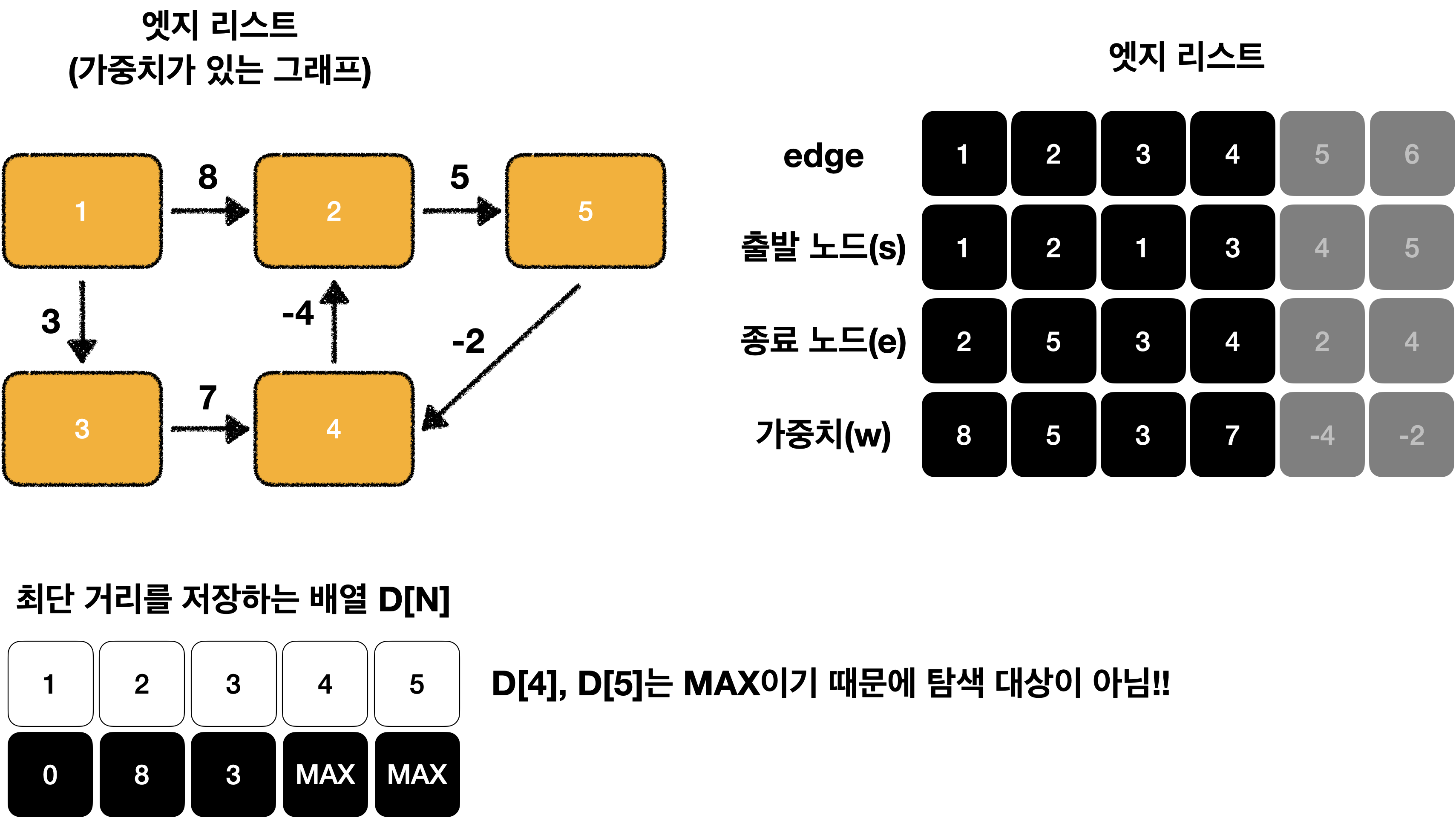
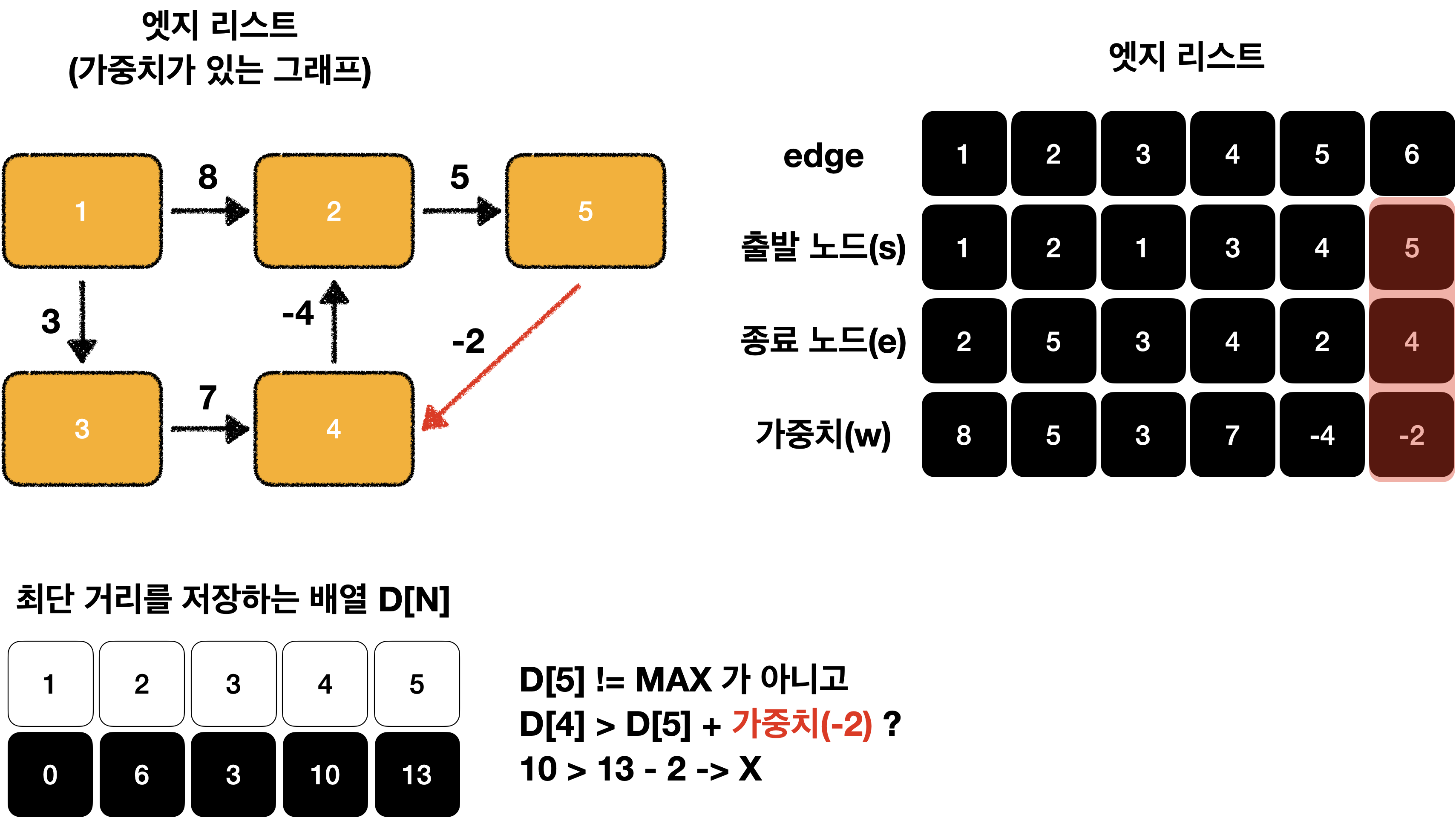
이어서 해보겠습니다.
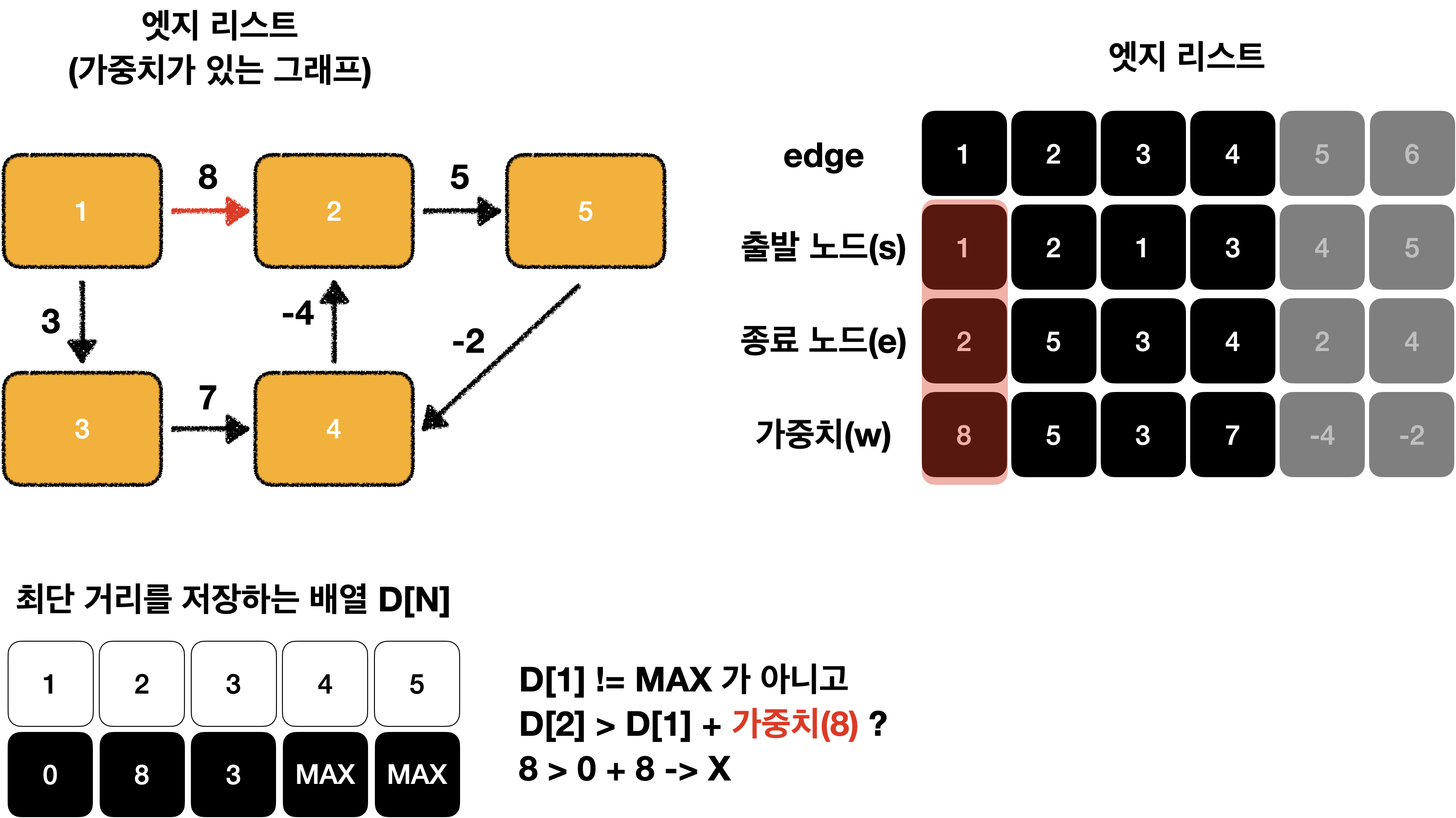
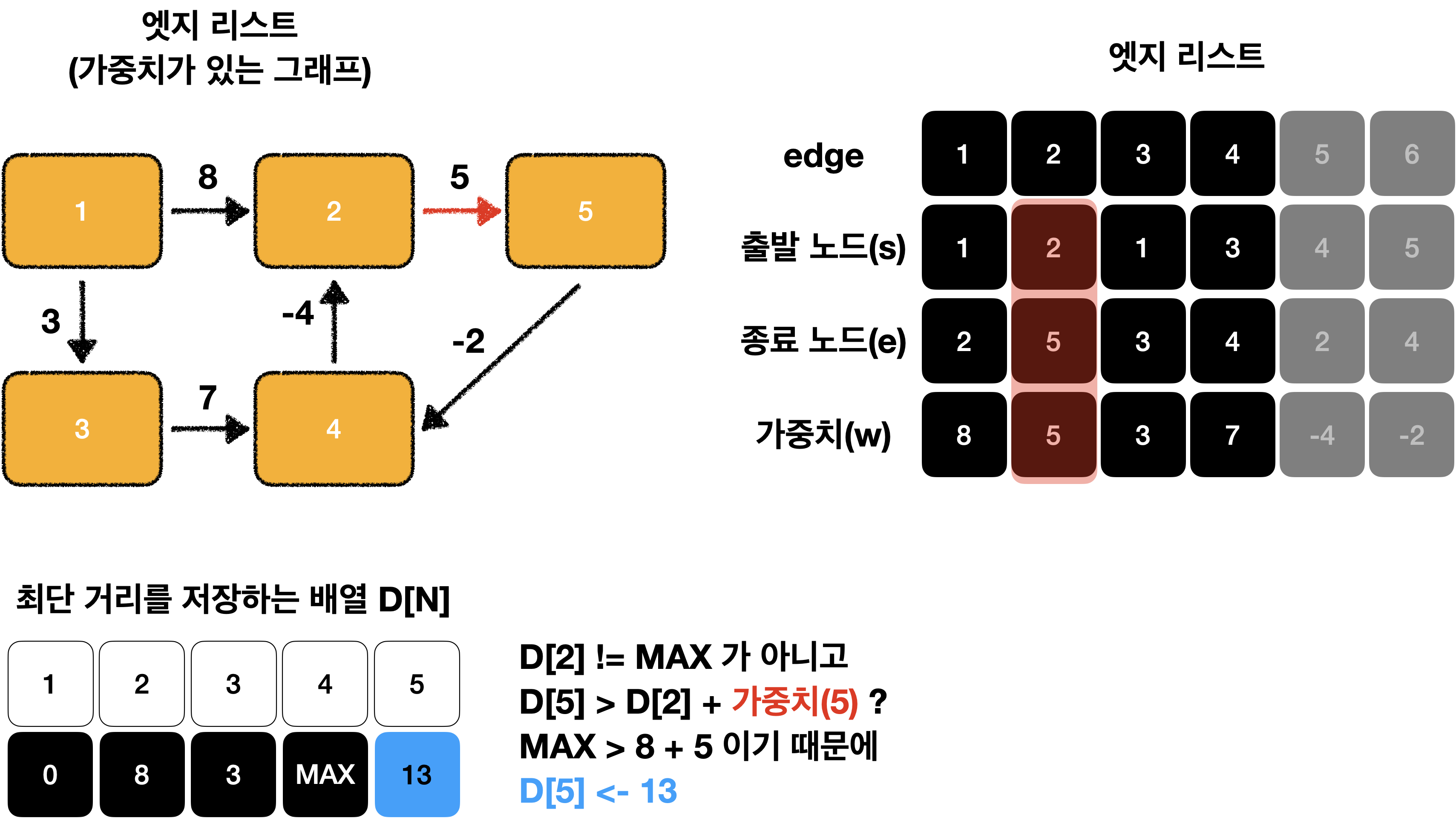
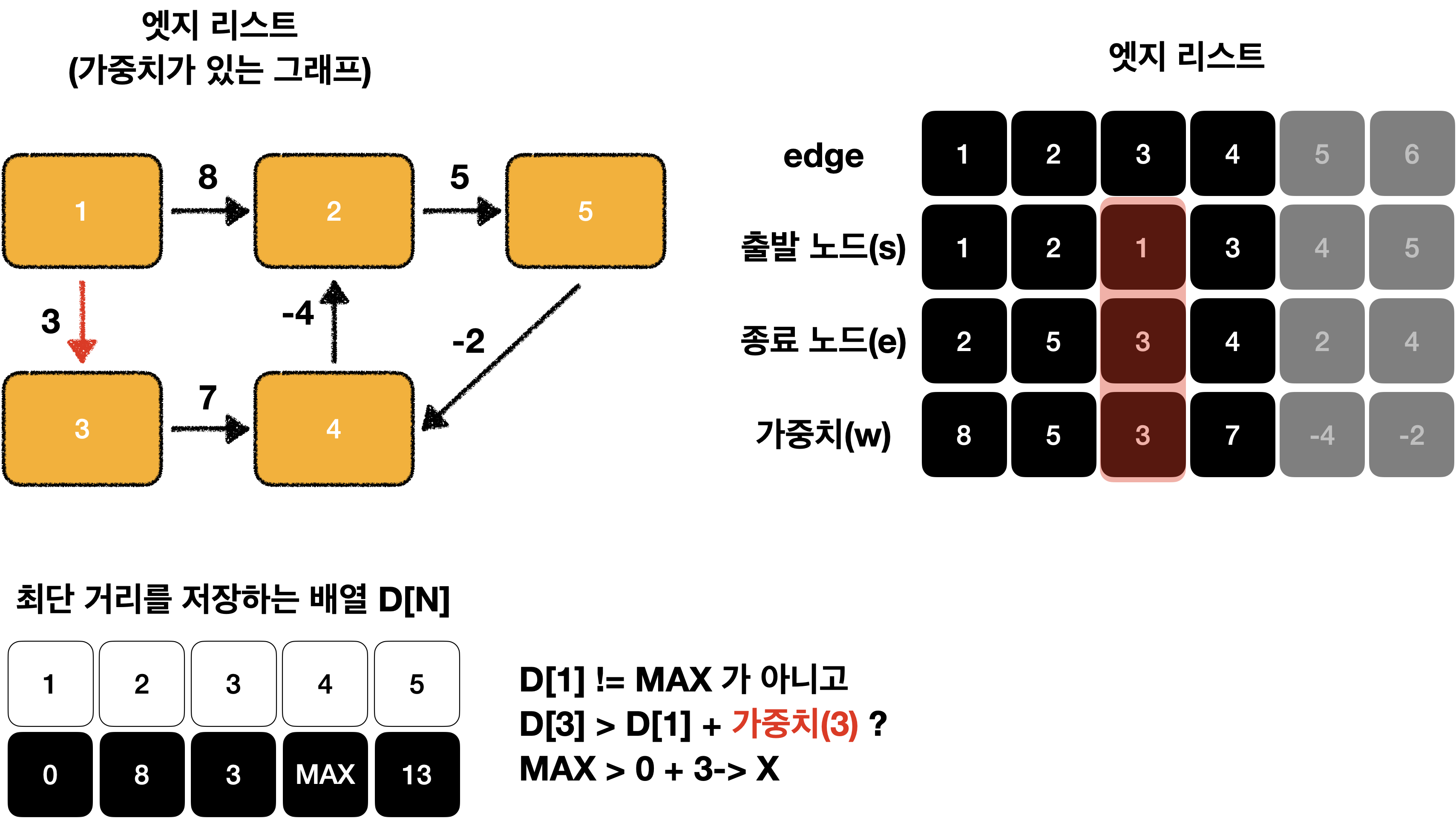
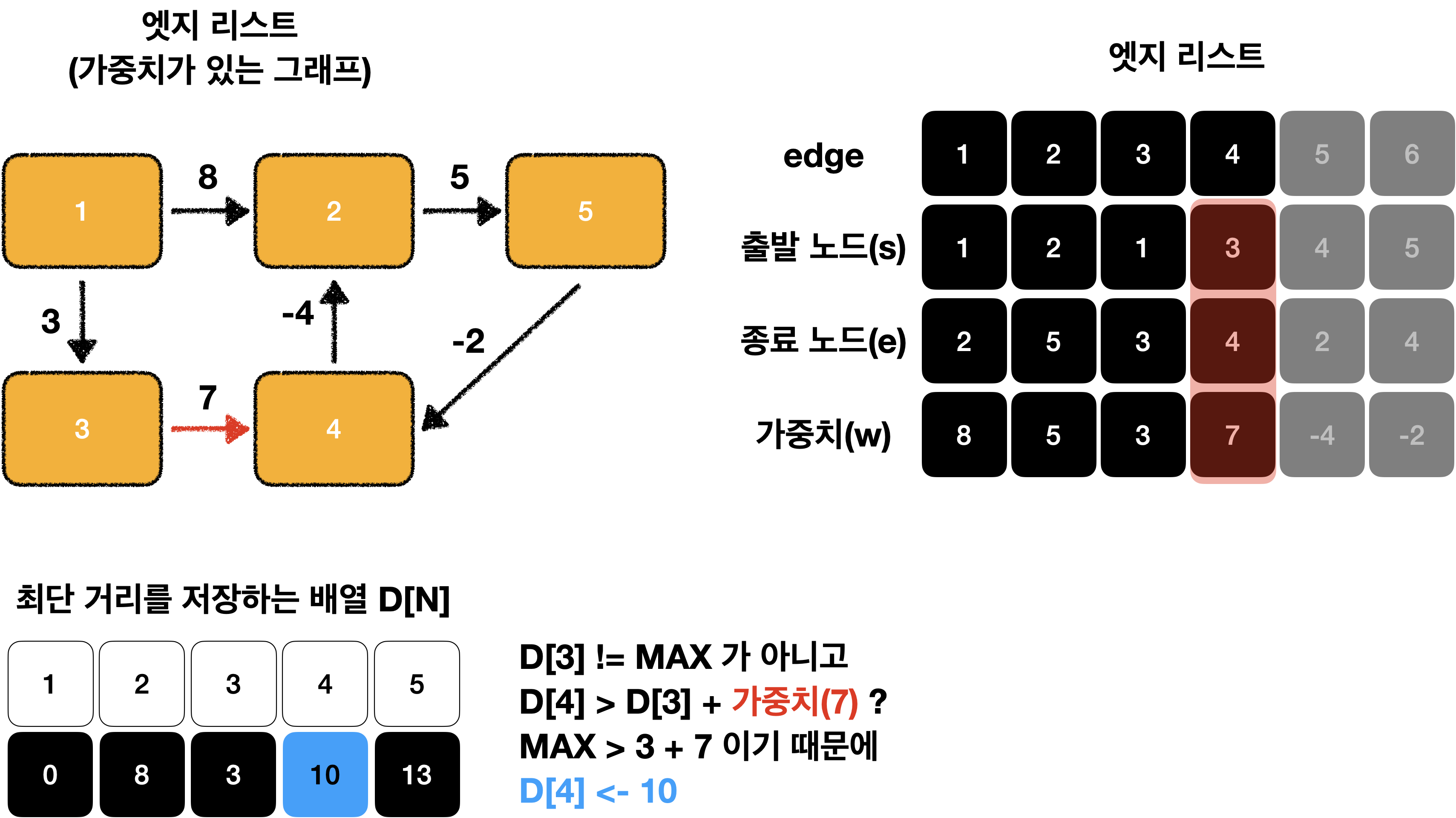
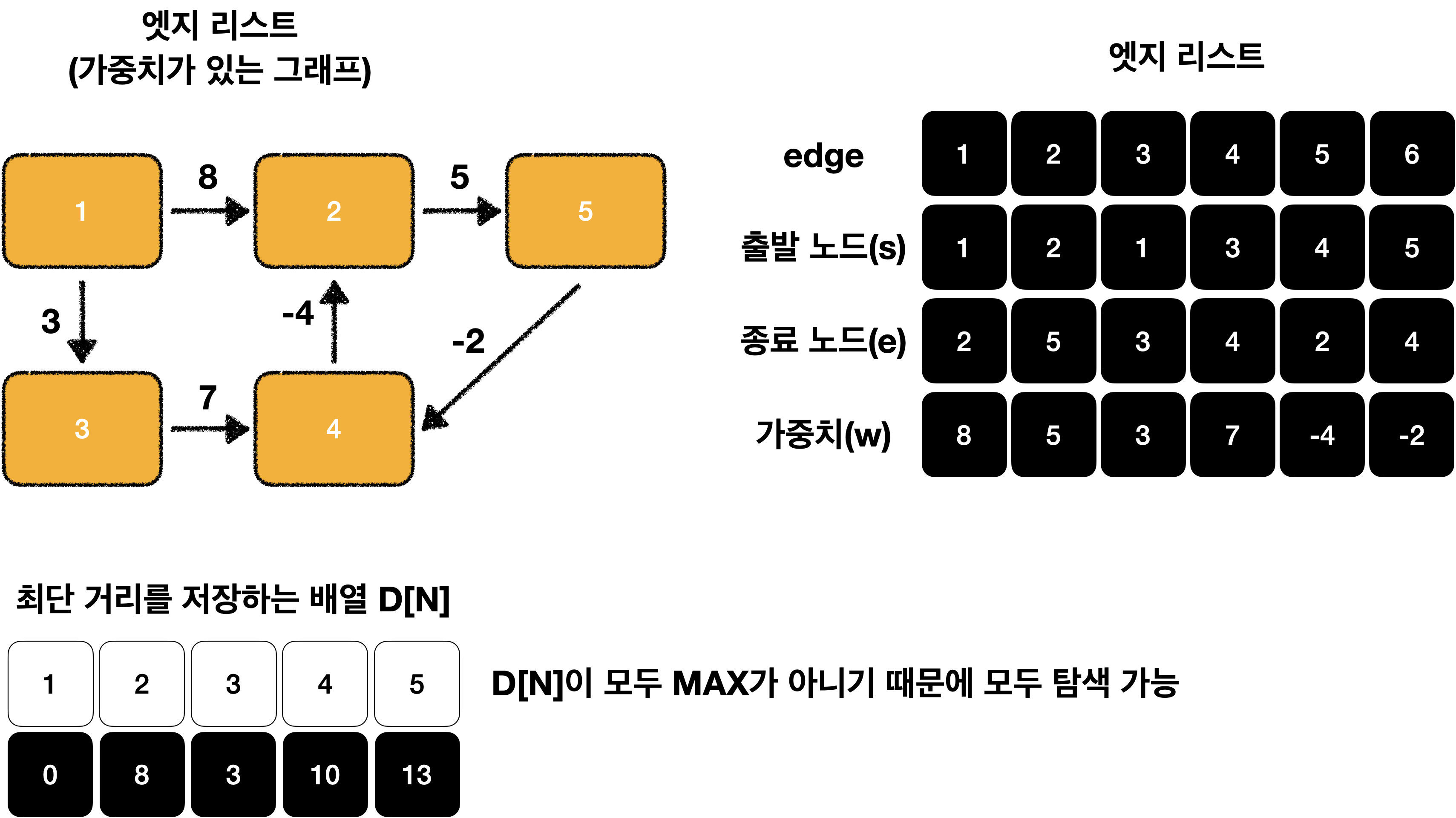
이제 D[N]이 모두 MAX가 아니기 때문에 모두 탐색이 가능한 것을 알 수 있습니다!😁
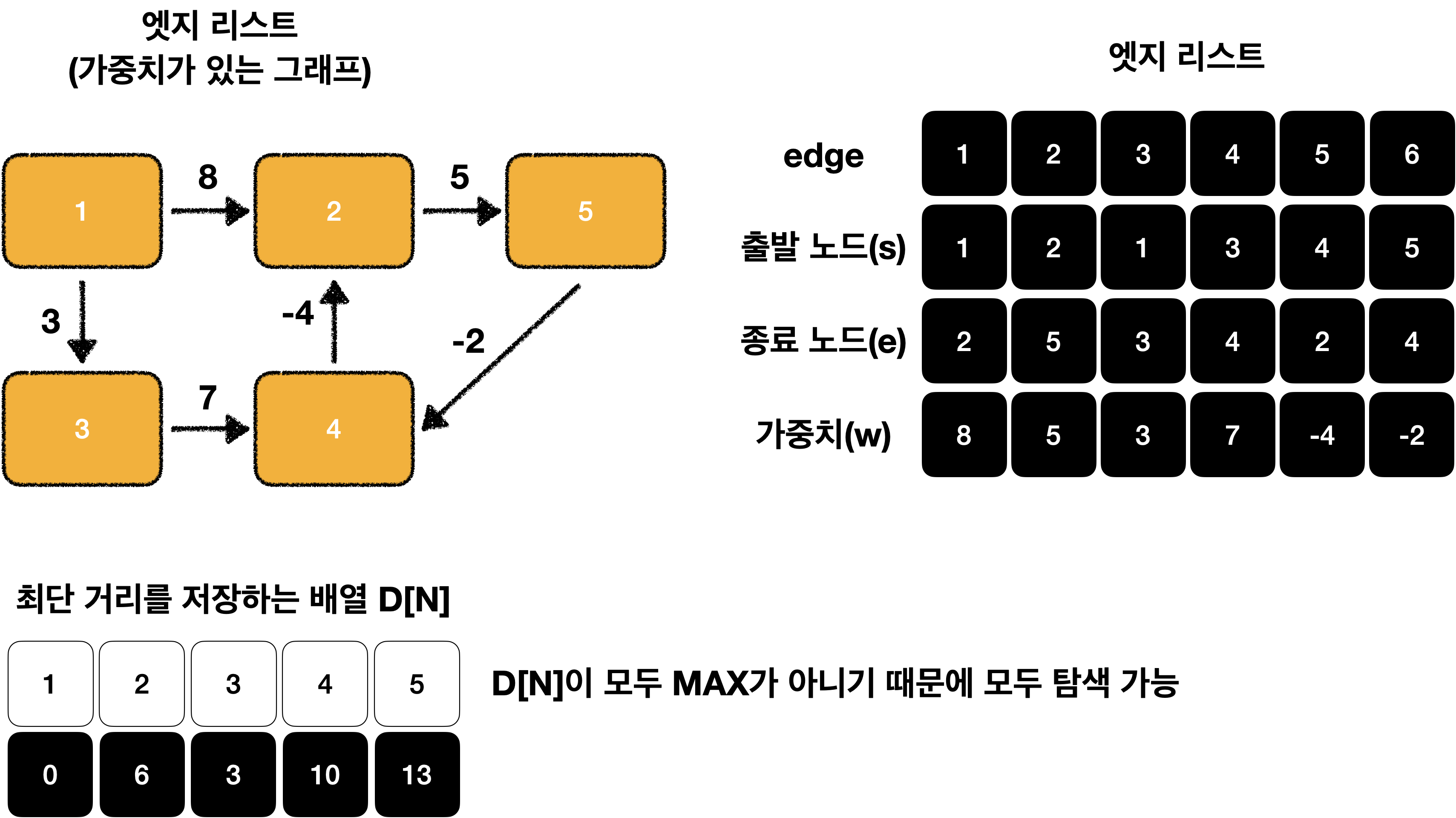
일부 생략…

최종 결과노드갯수 - 1 = 엣지 갯수 입니다.!!
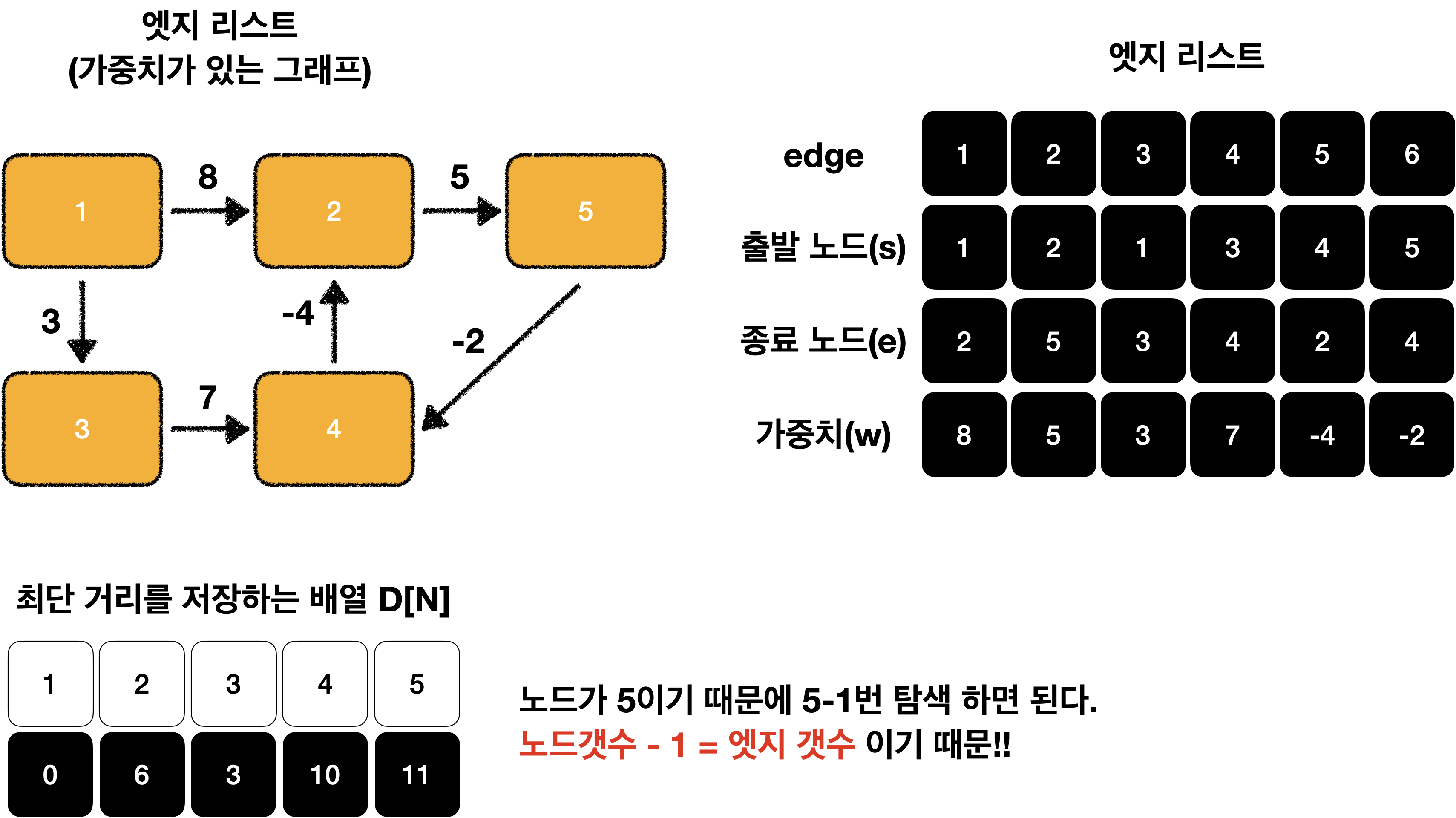
음수 사이클이 없을 때 N - 1 번 엣지 사용 횟수를 반복하면
출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 배열이 완성 됩니다.^^
마지막으로 이 그래프에 음수 사이클이 존재하는지 확인할 수 있는 방법이 무엇인지 알아봅시다!
✅음수 사이클 유무 확인
음수 사이클을 확인하기 위해 모든 엣지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하는지 확인 합니다.
만약 업데이트되는 노드가 있다면 음수 사이클이 있다는 의미! 입니다.
또한, 이전에 했던 정답 배열이 무의미하고 최단 거리를 찾을 수 없는 그래프라는 의미 입니다.
음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하기 때문입니다….!!
위에 그래프를 한 번 더 돌려봅시다🏃♀️
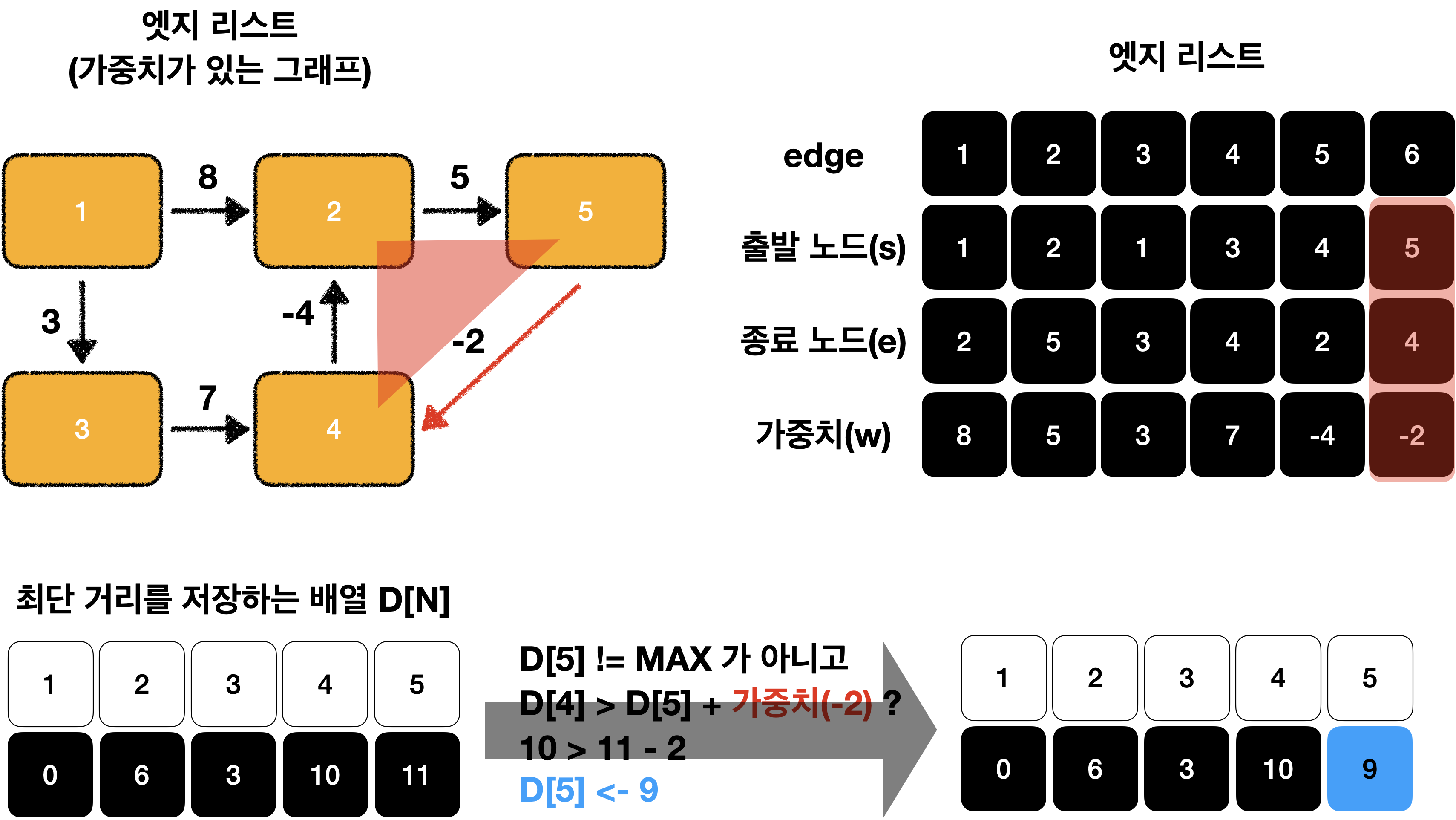
D[5]에서 업데이트가 발생 했습니다.
따라서 해당 노드는 음수 사이클이 존재하고 최단 거리를 찾을 수 없습니다…!
이제 실전 문제를 풀어봅시다~📚
백준 11657
출력초과가 발생해서 당황했던 문제 입니다. 😲
N = 500, M = 6000 인 경우 최대 3,000,000번의 loop를 돌게 됩니다.
이때 음의 간선이 -10,000이라면 약 -30,000,000,000의 값 입니다.
Java 에서 int는 2,147,483,647까지 표현할 수 있기 때문에9,223,372,036,854,775,807까지 표현 가능한 long을 사용합니다.
풀이
public class Quiz11657 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 도시 갯수
int n = Integer.parseInt(st.nextToken());
// 버스 노선 갯수
int m = Integer.parseInt(st.nextToken());
// 엣지 리스트
List<Bus> edgeList = new ArrayList<>();
// 그래프로 표현
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList.add(new Bus(start, end, weight));
}
// 최단 거리 배열
long[] result = new long[n+1];
for(int i = 1; i <= n; i++) {
result[i] = Long.MAX_VALUE;
}
// 출발 노드
result[1] = 0;
// 최단 거리 업데이트 횟수는 노드 갯수 - 1
for(int i = 0; i < n - 1; i++) {
// 엣지의 갯수만큼 탐색
for(int j = 0; j < m; j++) {
Bus bus = edgeList.get(j);
if(result[bus.getStart()] != Long.MAX_VALUE
&& result[bus.getEnd()] > result[bus.getStart()] + bus.getWeight()) {
result[bus.getEnd()] = result[bus.getStart()] + bus.getWeight();
}
}
}
// 음수 사이클 존재 확인(엣지를 한번 씩 사용해서 업데이트 유무 확인)
if(isMinusCycle(m, edgeList, result)) {
System.out.print(-1);
br.close();
return;
}
// 음수 사이클이 없으면
// 1 -> 2, 1 -> 3, 1 -> 4 ... 최단 거리 출력
StringBuilder sb = new StringBuilder();
for(int i = 2; i <= n; i++) {
// 경로가 없으면 -1 출력
if (result[i] == Long.MAX_VALUE) {
sb.append(-1).append("\n");
} else {
sb.append(result[i]).append("\n");
}
}
System.out.print(sb);
br.close();
}
// 음수 사이클 존재 확인(엣지를 한번 씩 사용해서 업데이트 유무 확인)
private static boolean isMinusCycle(int m, List<Bus> edgeList, long[] result) {
for(int j = 0; j < m; j++) {
Bus bus = edgeList.get(j);
if(result[bus.getStart()] != Long.MAX_VALUE
&& result[bus.getEnd()] > result[bus.getStart()] + bus.getWeight()) {
return true;
}
}
return false;
}
static public class Bus {
private int start;
private int end;
private int weight;
public Bus(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getWeight() {
return weight;
}
}
}백준 1865
이 문제를 푸는 방법은 2가지 입니다.
- 모든 정점을 출발점으로 조사해서
cycle의 유무를 파악하는 방법. - 이 알고리즘에서
cycle의 형성 유무에 대해서 잘 생각해보기
글 읽기 - INF비교가 없어야 하는 이유가 뭘까요?
혼자 해결하지 못했습니다..
벨만-포드 알고리즘은 출발점이 특정한 한 점일때 가능한 알고리즘이기 때문에
처음에 출발 노드를 임의로 선정하고, 음수 사이클이 발생하는지 확인하면 되는 문제인줄 알았지만
문제에서 노드 끼리 반드시 연결된다는 말이 없기 때문에
출발 노드를 임의로 선정하면 안됩니다.!!
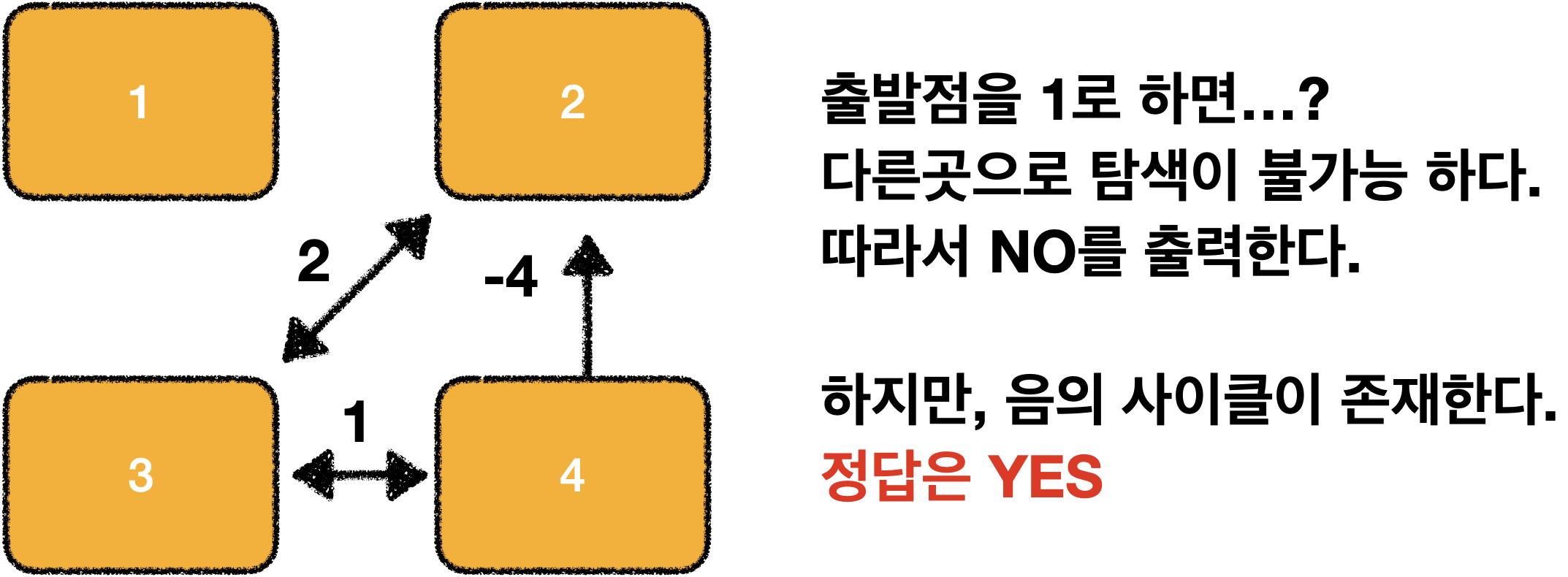
따라서 모든 점을 출발점으로 벨만-포드 알고리즘으로 검증한다.
추가로 시간 단축을 위해 벨만-포드 탐색 과정에 flag를 만들었다.
for(int i = 0; i < n - 1; i++) {
boolean flag = false;
// 엣지 갯수만큼 실행
for(int j = 0; j < edgeList.size(); j++) {
int start = edgeList.get(j).getStart();
int end = edgeList.get(j).getEnd();
int time = edgeList.get(j).getTime();
if(result[start] != Long.MAX_VALUE
&& result[end] > result[start] + time) {
// 최단거리 계산
result[end] = result[start] + time;
flag = true;
}
}
// 갱신이 더 이상 안되면 탈출!
if(!flag) {
break;
}
}
풀이
public class Quiz1865 {
public static void main(String[] args) throws IOException {
/**
* 2 // 테스트 케이스 갯수
* 3 3 1 1 // 지점갯수, 도로 갯수(m:3), 웜홀 갯수(w:1)
* 1 2 2 2 // 도로 정보 (시작점, 끝점, 걸리는 시간) 2부터 m+1 까지
* 1 3 4 3 // 도로 정보 (시작점, 끝점, 걸리는 시간)
* 2 3 1 4 // 도로 정보 (시작점, 끝점, 걸리는 시간)
* 3 1 3 5 // 웜홀 정보 (시작점, 끝점, 걸리는 시간) m+2(5)부터 m+w+1(5) 까지
* 3 2 1 1 // 지점갯수, 도로 갯수(m:2), 웜홀 갯수(w:1)
* 1 2 3 2 // 도로 정보 (시작점, 끝점, 걸리는 시간) 2부터 m+1 까지
* 2 3 4 3 // 도로 정보 (시작점, 끝점, 걸리는 시간) 2부터 m+1 까지
* 3 1 8 4 // 웜홀 정보 (시작점, 끝점, 걸리는 시간) m+2(4)부터 m+w+1(4) 까지
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int tc = Integer.parseInt(br.readLine());
for(int t = 0; t < tc; t++) {
StringTokenizer st = new StringTokenizer(br.readLine());
// 지점의 수
int n = Integer.parseInt(st.nextToken());
// 도로 갯수
int m = Integer.parseInt(st.nextToken());
// 웜홀 갯수
int w = Integer.parseInt(st.nextToken());
// 도로는 방향이 없고, 웜홀은 방향이 있음
// 엣지 리스트
List<Node> edgeList = new ArrayList<>();
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
// 시작점
int start = Integer.parseInt(st.nextToken());
// 끝점
int end = Integer.parseInt(st.nextToken());
// 걸리는 시간
int time = Integer.parseInt(st.nextToken());
// 양 방향
edgeList.add(new Node(start, end, time));
edgeList.add(new Node(end, start, time));
}
for(int i = 0; i < w; i++) {
st = new StringTokenizer(br.readLine());
// 시작점
int start = Integer.parseInt(st.nextToken());
// 끝점
int end = Integer.parseInt(st.nextToken());
// 걸리는 시간
int time = Integer.parseInt(st.nextToken());
// 단방향
edgeList.add(new Node(start, end, time * -1));
}
// 한 지점에서 출발해서, 시간이 줄면서 출발위치로 돌아오는게 가능한지
// 이말은 음수 사이클이 존재하는지 파악 하면된다.
// 그런데 노드끼리 연결되지 않은 노드가 있을 수 있다.
// 따라서 아무 노드를 출발점으로 하면 안되고, 모든 노드를 테스트 해본다.
// 노드 갯수만큼 실행
boolean flag = false;
for(int k = 1; k <= n; k++) {
if(bellmanFord(k, n, edgeList)) {
sb.append("YES").append("\n");
flag = true;
break;
}
}
if(!flag) {
sb.append("NO").append("\n");
}
}
System.out.print(sb);
br.close();
}
private static boolean bellmanFord(int k, int n, List<Node> edgeList) {
// 최단거리 초기화
long[] result = new long[n+1];
for(int i = 1; i <= n; i++) {
result[i] = Long.MAX_VALUE;
}
// 시작 노드
result[k] = 0;
for(int i = 0; i < n - 1; i++) {
boolean flag = false;
// 엣지 갯수만큼 실행
for(int j = 0; j < edgeList.size(); j++) {
int start = edgeList.get(j).getStart();
int end = edgeList.get(j).getEnd();
int time = edgeList.get(j).getTime();
if(result[start] != Long.MAX_VALUE
&& result[end] > result[start] + time) {
// 최단거리 계산
result[end] = result[start] + time;
flag = true;
}
}
if(!flag) {
break;
}
}
// 음수 사이클 존재 확인
if(isMinusCycle(edgeList, result)) {
return true;
}
return false;
}
private static boolean isMinusCycle(List<Node> edgeList, long[] result) {
// 엣지 갯수만큼 실행
for (int j = 0; j < edgeList.size(); j++) {
int start = edgeList.get(j).getStart();
int end = edgeList.get(j).getEnd();
int time = edgeList.get(j).getTime();
if (result[start] != Long.MAX_VALUE
&& result[end] > result[start] + time) {
// 음수 사이클 존재!
return true;
}
}
return false;
}
static class Node {
private int start;
private int end;
private int time;
public Node(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getTime() {
return time;
}
}
}
벨만-포드 알고리즘은 출발점이 특정한 한 점일때 가능한 알고리즘 입니다.
벨만-포드 에서 cycle 형성이 언제 되는지 확인해봅시다.
먼저 MAX로 초기화 하는 이유는 단절 되었다를 표시하거나,
어떤 지점으로 부터 거리를 구하기 위해서 설정합니다.(거리를 모르기 때문에 무한대라고 표기하는 것)
따라서 단순 그래프에서의 음의 사이클 유무만 파악할 때는 result[]의 초기화를 어떤 값으로 해주어도 상관 없습니다.
그 이유는 거리를 구하는게 아니라 음의 사이클이 존재할 때, 변화만 파악하면 되기 때문입니다.!!!
따라서 reulst[]의 초기값을 -1 이나, 987,654,321 같은 적절한 값으로 초기화 한 뒤,
벨만 포드 알고리즘을 수행하면 음의 사이클을 찾을 수 있습니다.
풀이2
public class Quiz1865_2 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int tc = Integer.parseInt(br.readLine());
for(int t = 0; t < tc; t++) {
StringTokenizer st = new StringTokenizer(br.readLine());
// 지점의 수
int n = Integer.parseInt(st.nextToken());
// 도로 갯수
int m = Integer.parseInt(st.nextToken());
// 웜홀 갯수
int w = Integer.parseInt(st.nextToken());
// 도로는 방향이 없고, 웜홀은 방향이 있음
// 엣지 리스트
List<Node> edgeList = new ArrayList<>();
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
// 시작점
int start = Integer.parseInt(st.nextToken());
// 끝점
int end = Integer.parseInt(st.nextToken());
// 걸리는 시간
int time = Integer.parseInt(st.nextToken());
// 양 방향
edgeList.add(new Node(start, end, time));
edgeList.add(new Node(end, start, time));
}
for (int i = 0; i < w; i++) {
st = new StringTokenizer(br.readLine());
// 시작점
int start = Integer.parseInt(st.nextToken());
// 끝점
int end = Integer.parseInt(st.nextToken());
// 걸리는 시간
int time = Integer.parseInt(st.nextToken());
// 단방향
edgeList.add(new Node(start, end, time * -1));
}
// 적절한 값으로 최단거리 배열 초기화
// 단순 그래프에서의 사이클 유무만 파악할 때는 result[]의 초기화를 어떤 값으로 해주어도 상관 없습니다.
// 거리를 구하는게 아니라 음의 사이클이 존재할 때, 변화만 파악하면 되기 때문
long[] result = new long[n+1];
for(int i = 1; i < n; i++) {
result[i] = 987654321;
}
// 출발 노드 설정
result[1] = 0;
bellmanFord(n, edgeList, result);
if(isMinusCycle(edgeList, result)) {
sb.append("YES").append("\n");
} else {
sb.append("NO").append("\n");
}
}
System.out.print(sb);
br.close();
}
private static void bellmanFord(int n, List<Node> edgeList, long[] result) {
for(int i = 0; i < n - 1; i++) {
boolean flag = false;
for(Node node : edgeList) {
int start = node.getStart();
int end = node.getEnd();
int time = node.getTime();
// 거리를 구하는게 아니라 음의 사이클이 존재할 때, 변화만 파악하면 되기 때문에
// result[start] != INF 가 없어도 된다~
if(result[end] > result[start] + time) {
result[end] = result[start] +time;
flag = true;
}
}
if (!flag) {
break;
}
}
}
// 음의 사이클 존재 확인
private static boolean isMinusCycle(List<Node> edgeList, long[] result) {
for(Node node : edgeList) {
int start = node.getStart();
int end = node.getEnd();
int time = node.getTime();
if(result[end] > result[start] + time) {
return true;
}
}
return false;
}
static class Node {
private int start;
private int end;
private int time;
public Node(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getTime() {
return time;
}
}
}

백준 1219
좀 많이 어려웠다.😭
그 이유는 고려해야할 조건이 많았습니다.
먼저 단순하게 음의 사이클이 발생하면 무한대로 돈을 벌 수 있다. 라고 생각해서 Gee 를 출력했습니다.
결과는 틀렸습니다.^^ ㅎㅎㅎ
왜냐하면
문제의 그래프에서 음의 사이클이 발생 하지만
우리가 원하는 도착 노드에서 음의 사이클이 발생하는지 모르기 때문입니다.
아래 그림을 보면 이해가 쉬울 것 입니다.^^

돈을 무한으로 벌기 위해서는 음의 사이클이 발생하는 지점에서 도착지점과 연결되어 있어야 합니다.
따라서 음의 사이클이 발생하는 노드를 저장하고,
이를 bfs를 이용해서 노드가 연결되어 있는지 확인 했습니다.
풀이
public class Quiz1219 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 도시 갯수
int n = Integer.parseInt(st.nextToken());
// 시작 도시
int startCity = Integer.parseInt(st.nextToken());
// 도착 도시
int endCity = Integer.parseInt(st.nextToken());
// 교통 수단 갯수
int m = Integer.parseInt(st.nextToken());
List<City> list = new ArrayList<>();
// 엣지에 발생하는 비용
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int paid = Integer.parseInt(st.nextToken());
list.add(new City(start, end, paid));
}
// 노드에 방문하면 발생하는 수익
st = new StringTokenizer(br.readLine());
List<Integer> profits = new ArrayList<>();
for(int i = 0; i < n; i++) {
int profit = Integer.parseInt(st.nextToken());
profits.add(profit);
}
// 최단 거리 초기화
long[] result = new long[n];
for(int i = 0; i < n; i++) {
result[i] = Long.MAX_VALUE;
}
// 출발 도시
result[startCity] = profits.get(startCity) *(-1L);
// 최단 거리 탐색
bellmanFord(n, m, list, profits, result);
// 음의 사이클이 발생하는 노드 저장 리스트
List<Integer> minusCycleNode = new ArrayList<>();
StringBuilder sb = new StringBuilder();
long value = result[endCity];
// 도착 지점에 갈 수 없는 경우
if(value == Long.MAX_VALUE) {
sb.append("gg");
}
// 음의 사이클이 발생하는 경우
else if(isMinusCycle(m, list, profits, result, minusCycleNode)) {
boolean flag = false;
for(Integer node : minusCycleNode) {
flag = bfs(node, endCity, list, n, m);
// 음의 사이클에서 종료 노드가 연결되어 있는 경우
if(flag) {
// 돈을 무한으로 벌 수 있다.
sb.append("Gee");
break;
}
}
if(!flag){
// 무한대로 돈 못번다.
sb.append(value*(-1));
}
}
// 음의 사이클이 발생하지 않는 경우
else {
// 무한대로 돈 못번다.
sb.append(value*(-1));
}
System.out.print(sb);
br.close();
}
// 음의 사이클이 발생했을 때 특정 두 도시가 연결되어있는지 확인
private static boolean bfs(int startCity, int endCity, List<City> list, int n, int m) {
if(startCity == endCity) {
return true;
}
Queue<Integer> q = new ArrayDeque<>();
// 방문 이력
boolean[] visited = new boolean[n];
q.offer(startCity);
visited[startCity] = true;
while (!q.isEmpty()) {
Integer currentNode = q.poll();
for(int i = 0; i < m; i++) {
City city = list.get(i);
int start = city.getStart();
int end = city.getEnd();
// 탐색 대상이면
if(start == currentNode) {
// 방문 이력이 없으면
if(!visited[end]) {
// 노드가 연결 되어 있으면
if(endCity == end) {
return true;
}
visited[end] = true;
q.add(end);
}
}
}
}
return false;
}
// 음의 사이클이 발생하는지
private static boolean isMinusCycle(int m, List<City> list, List<Integer> profits, long[] result, List<Integer> minusCycleNode) {
boolean flag = false;
// 음수 사이클 확인
for(int j = 0; j < m; j++) {
City city = list.get(j);
int start = city.getStart();
int end = city.getEnd();
int paid = city.getPaid();
// 해당 노드에 방문하면 발생하는 수익
int profit = profits.get(end);
// 해당 노드에 방문 했을 때 비용 계산
int money = paid - profit;
if (result[start] != Long.MAX_VALUE
&& result[end] > result[start] + money) {
// 음의 사이클이 발생하는 노드 정보 저장
minusCycleNode.add(start);
flag = true;
}
}
return flag;
}
private static void bellmanFord(int n, int m, List<City> list, List<Integer> profits, long[] result) {
// 노드 - 1 개 만큼 탐색
for(int i = 0; i < n + 100; i++) {
boolean flag = false;
// 엣지 갯수 만큼 탐색
for(int j = 0; j < m; j++) {
City city = list.get(j);
int start = city.getStart();
int end = city.getEnd();
int paid = city.getPaid();
// 해당 노드에 방문하면 발생하는 수익
int profit = profits.get(end);
// 해당 노드에 방문 했을 때 비용 계산
int money = paid - profit;
if(result[start] != Long.MAX_VALUE
&& result[end] > result[start] + money) {
result[end] = result[start] + money;
flag = true;
}
}
// 시간 복잡도 감소
if(!flag) {
break;
}
}
}
static class City {
private int start;
private int end;
private int paid;
public City(int start, int end, int paid) {
this.start = start;
this.end = end;
this.paid = paid;
}
public int getStart() {
return start;
}
public int getEnd() {
return end;
}
public int getPaid() {
return paid;
}
public void setMoney(int paid) {
this.paid = paid;
}
}
}
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 트리 기본 개념 (0) | 2023.04.12 |
|---|---|
| [알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386 -Java) (0) | 2023.04.10 |
| [알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java) (0) | 2023.04.02 |
| [알고리즘] 위상 정렬(백준 2252, 1766, 1516, 1005 -Java) (0) | 2023.04.02 |
| [알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java) (0) | 2023.03.29 |