[알고리즘] 위상 정렬(백준 2252, 1766, 1516, 1005 -Java)
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
위상 정렬

위상 정렬은 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘 입니다.
(유니온 파인드를 사용해서 사이클 유무를 판별하면 되겠죠?👍)
시간 복잡도는 O(V + E) 입니다.
위상 정렬에서는 항상 유일한 값으로 정렬되지 않습니다.
만약 사이클이 존재하면..? 🤔
노드 간의 순서를 명확하게 정의할 수 없기 때문에 위상 정렬을 적용할 수 없습니다.
위상 정렬 핵심 이론
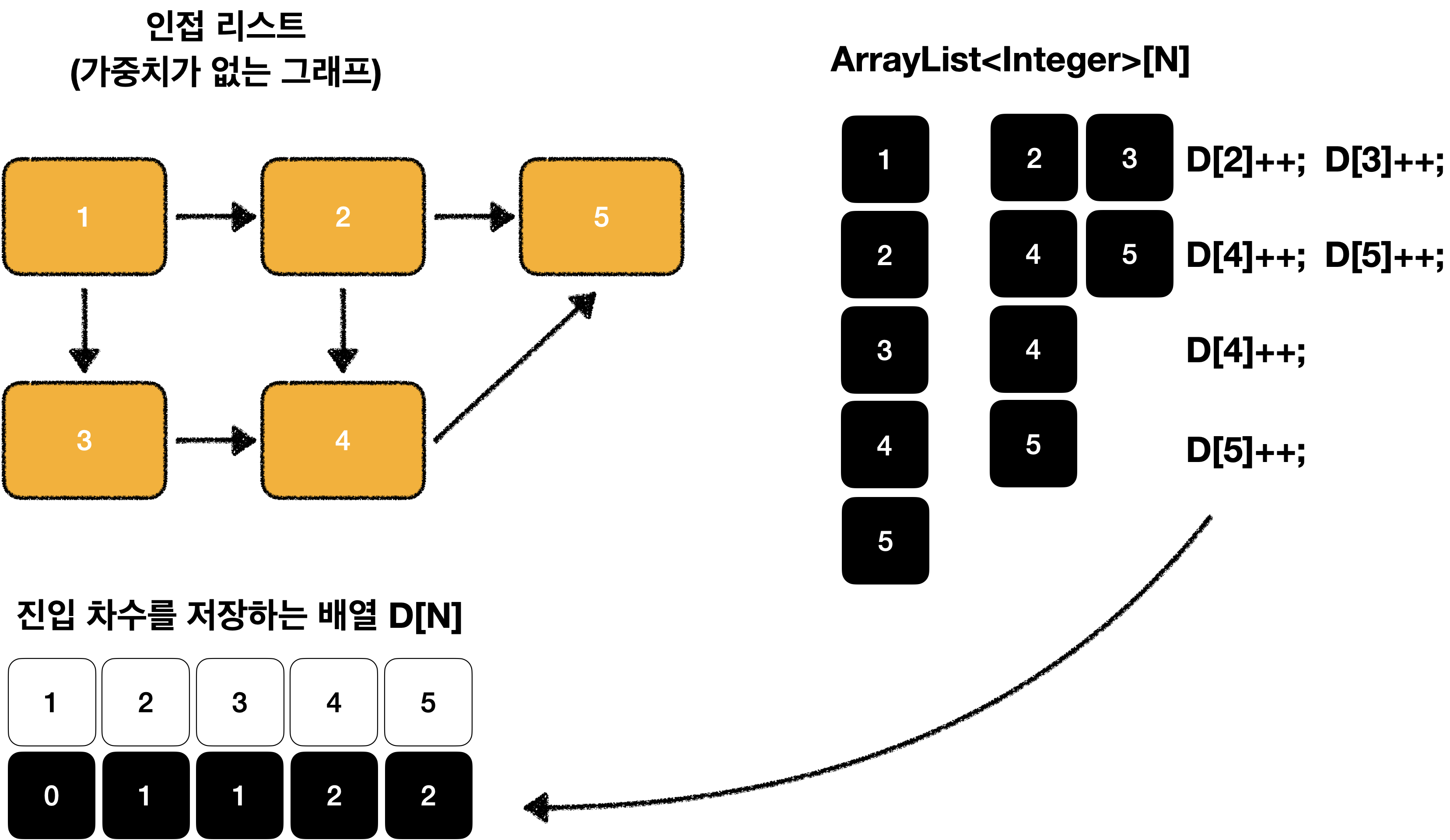
위상 정렬을 이해하기 위해서는 진입 차수의 개념을 알고 있어야 합니다.
진입 차수(in-dgree)는 자기 자신을 가리키는 엣지의 갯수 입니다.

먼저, 문제에서 주어진 데이터를 아래와 같은 자료구조로 표현할 수 있습니다.
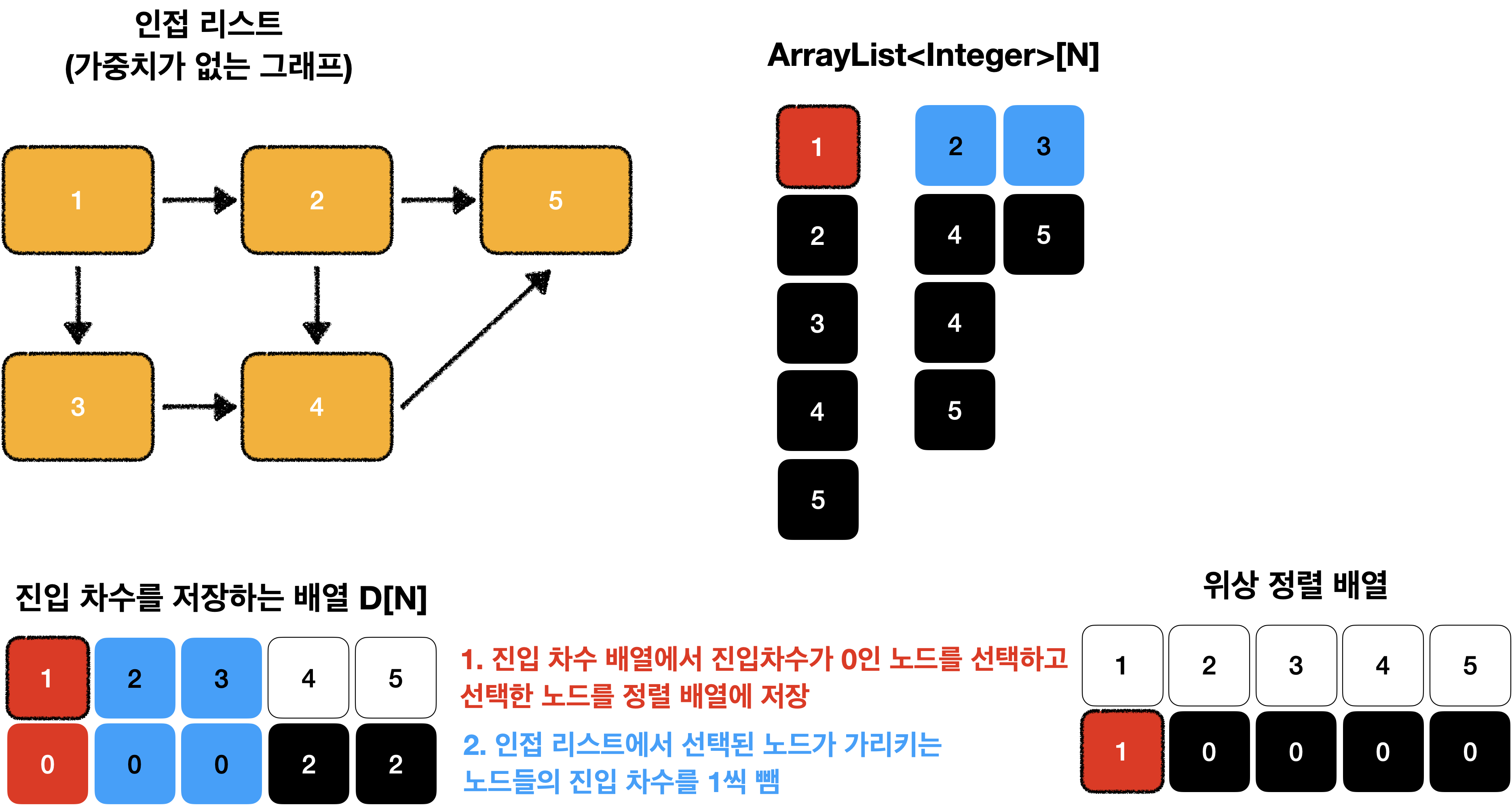
진입 차수 배열에서 진입 차수가 0인 노드를 선택하고 선택된 노드를 정렬 배열에 저장합니다.
그 후에 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 1씩 뺍니다.
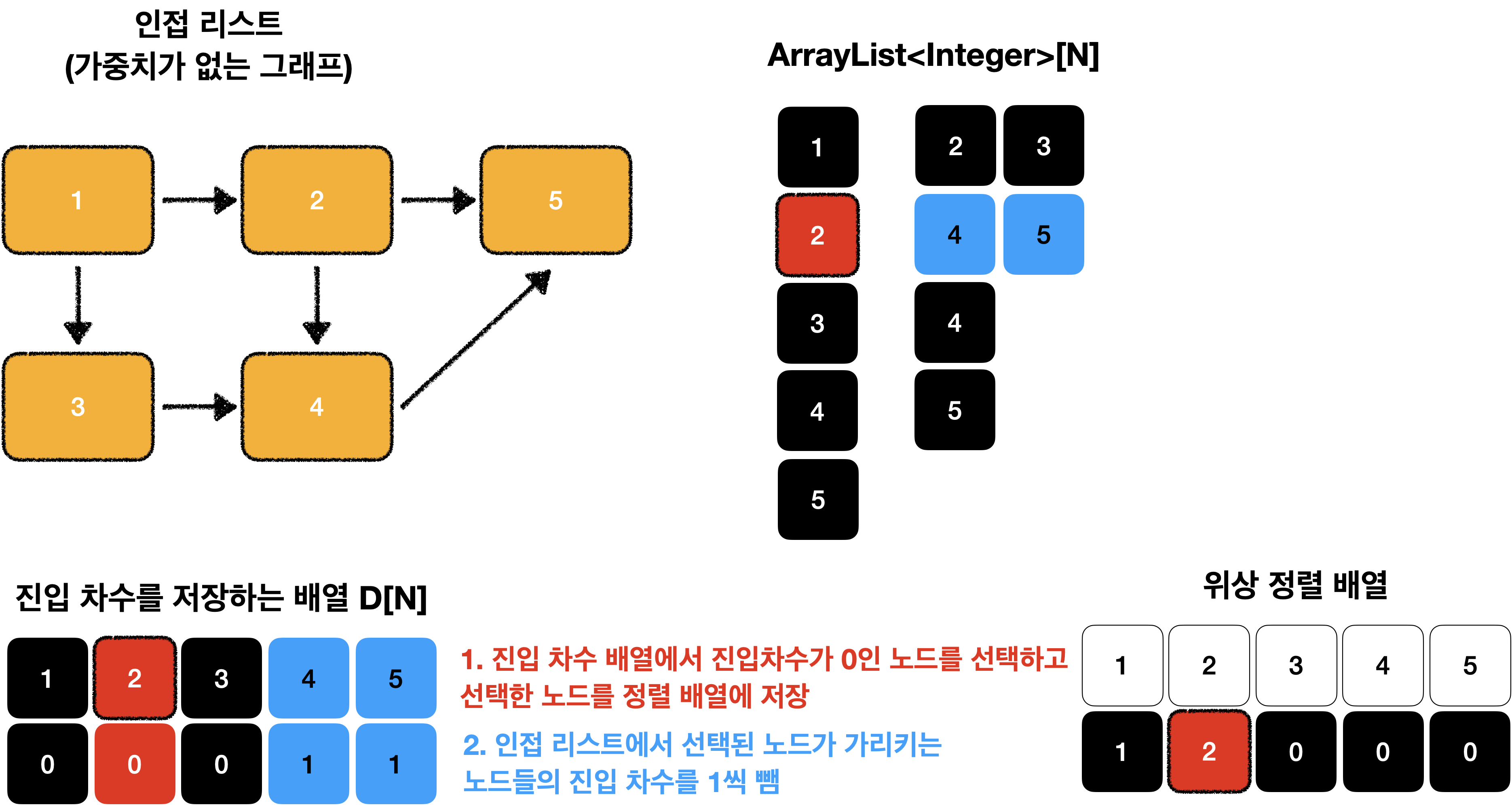
이 과정을 노드의 갯수만큼 반복 합니다.
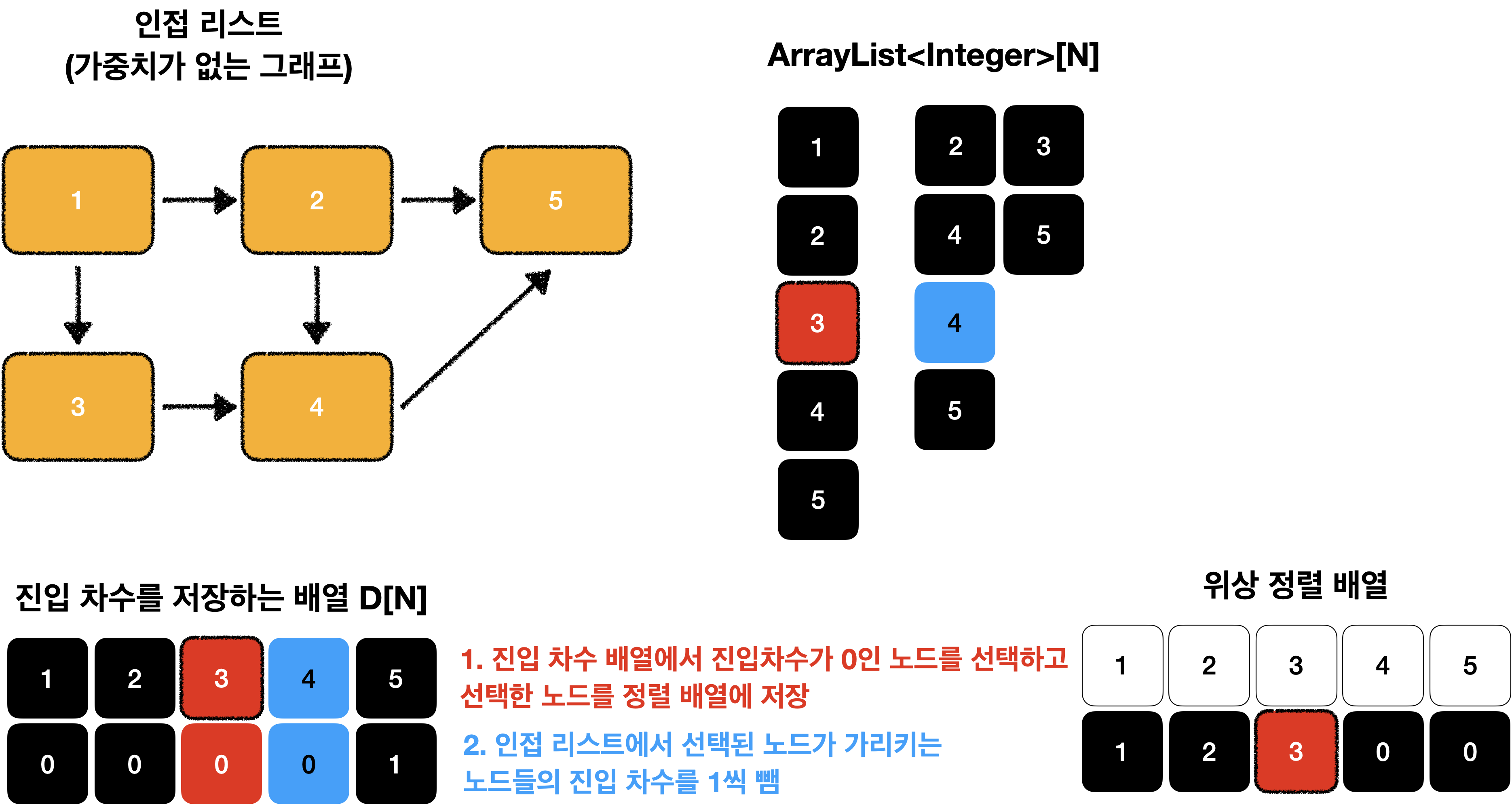
이때 2, 3 중 아무거나 선택해도 상관 없습니다.
따라서 위상 정렬은 항상 유일한 값으로 저장되지 않습니다.
정렬 결과가 여러개 일 수도 있다는 말 입니다.!!!!
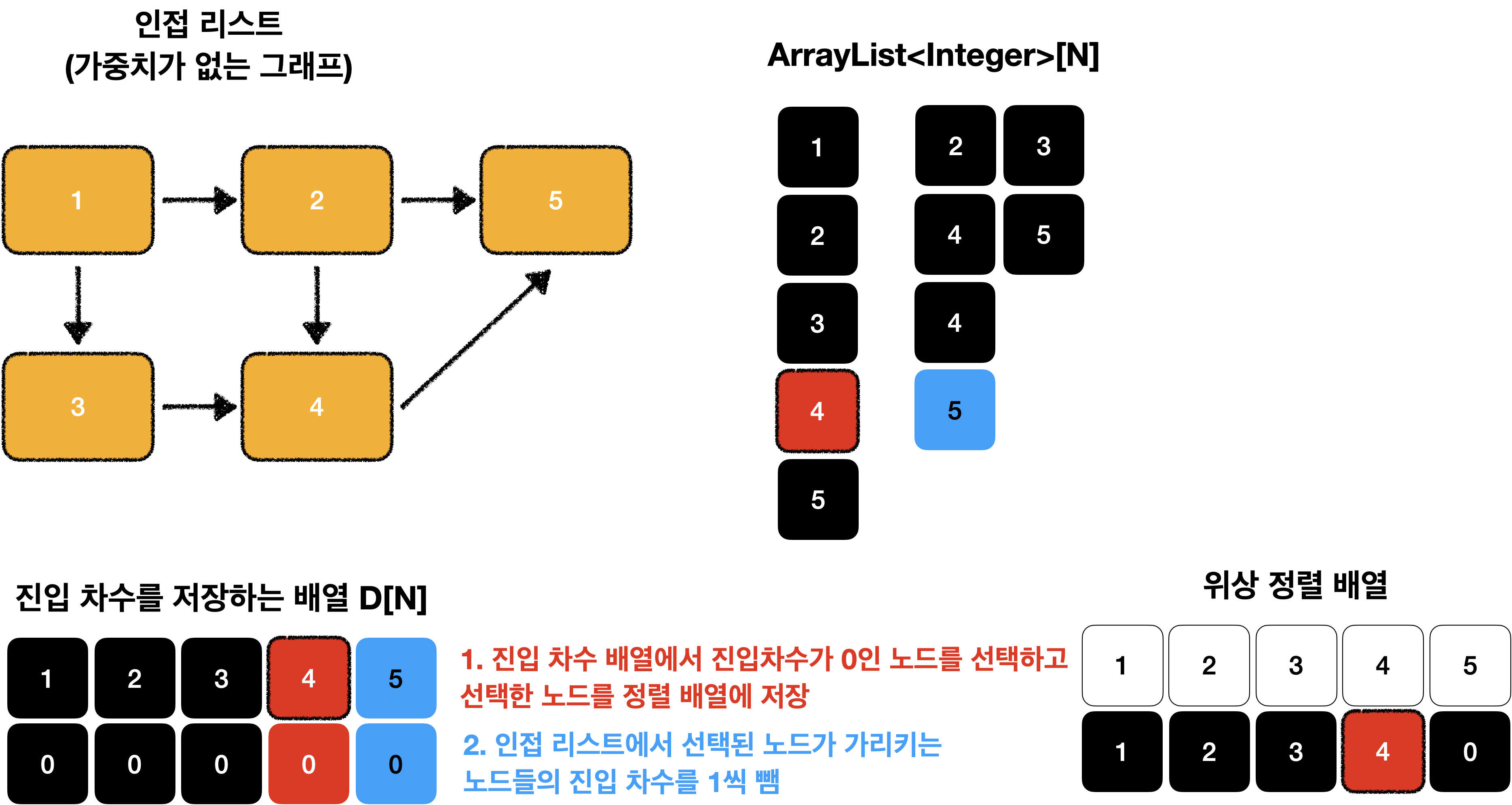
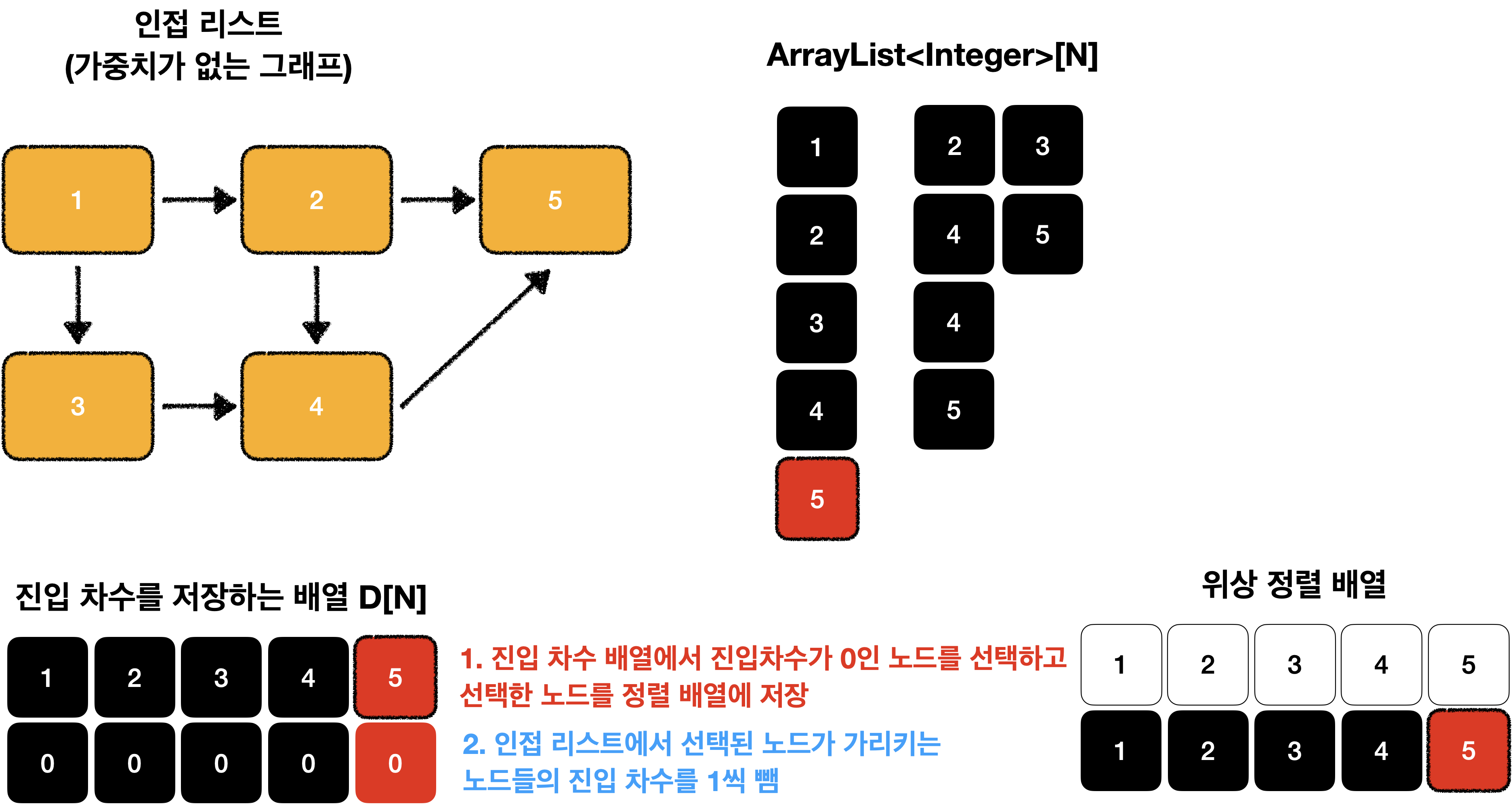
위상 정렬은 진입 차수 배열을 기준으로 알고리즘이 동작 합니다.!!
즉, 진입 차수를 이용한 정렬 입니다.
백준 2252
학생들을 노드로 생각하고, 키 순서 비교 데이터로 엣지를 만든다고 생각하면 됩니다.
그리고 답이 여러 가지일 경우에는 아무거나 출력한다라고 했기 때문에, 위상 정렬을 이용해서 풀면 됩니다.!
진입 차수가 0인 노드를 찾고 위상 정렬을 하는 과정에서
저는 처음에 진입 차수 방문 이력 배열을 만들어서 해결했습니다.
이런 방법으로 하면 문제는 node를 1로 초기화 하기 때문에 다시 N번 탐색해야해서 시간 복잡도가 증가합니다… 😭
int node = 1;
// 진입차수 방문 이력 배열
boolean[] visited = new boolean [n+1];
// 위상 정렬
while(result.size() < n) {
int degree = inDegree[node];
// 진입 차수가 0이면
if(degree == 0 && !visited[node]) {
// 노드를 정렬 배열에 저장
result.add(node);
// 노드의 인접 노드의 진입 차수를 1씩 감소
for(Integer j : list[node]) {
inDegree[j]--;
}
visited[node] = true;
// 초기화(노드 1부터 다시 탐색)
node = 1;
} else {
node++;
}
}
따라서 시간 복잡도를 감소시키기 위해서는 다른 방법이 필요했습니다….🤔
저의 머리로는 방법을 생각하지 못했습니다…🤯
방법은 진입 차수가 0을 저장하는 큐를 생성하는 것 입니다.!👍
// 진입 차수가 0인 노드를 큐에 넣기
Queue<Integer> queue = new ArrayDeque<>();
for(int i = 1; i <= n; i++) {
// 진입 차수가 0 이면
if(inDegree[i] == 0) {
queue.add(i);
}
}
풀이
public class Quiz2252 {
/**
* 3 2 // 학생 수, 키 비교 횟수
* 1 3 // 1이 3보다 앞에 서야함 1 -> 3
* 2 3 // 2가 3보가 앞에 서야함 2 -> 3
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 학생 수
int n = Integer.parseInt(st.nextToken());
// 키 비교 횟수
int m = Integer.parseInt(st.nextToken());
// 정렬 배열
List<Integer> result = new ArrayList<>();
// 진입 차수 배열
int[] inDegree = new int[n+1];
// 인접 리스트 초기화
List<Integer>[] list = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
// 인접 리스트 생성, 진입차수 배열 생성
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
// node1이 node2보다 앞에 서야함
// node1 -> node2
list[node1].add(node2);
inDegree[node2]++; // 인접노드의 진입차수 증가
}
// 진입 차수가 0인 노드를 큐에 넣기
Queue<Integer> queue = new ArrayDeque<>();
for(int i = 1; i <= n; i++) {
// 진입 차수가 0 이면
if(inDegree[i] == 0) {
queue.add(i);
}
}
StringBuilder sb = new StringBuilder();
// 위상 정렬
while(!queue.isEmpty()) {
int node = queue.poll();
// 노드를 정렬 배열에 저장
result.add(node);
sb.append(node).append(" ");
// 노드의 인접 노드의 진입 차수를 1씩 감소
for(Integer j : list[node]) {
inDegree[j]--;
// 노드의 진입 차수가 0 이면
if(inDegree[j] == 0) {
// 큐에 노드 삽입
queue.add(j);
}
}
}
System.out.print(sb);
br.close();
}
}
2,200ms넘게 단축된것을 확인 할 수 있습니다!! 👍
백준 1766
문제에서 가능한 쉬운 문제부터 해결해야 한다고 했습니다.
따라서 저는 우선순위 큐를 사용하여 문제를 해결했습니다.
(우선순위 큐의 기본 설정은 오름차순 입니다. 오름차순은 작은 값에서 시작하여 끝울 큰 값으로 정렬하는 것을 의미합니다.^^)
풀이
public class Quiz1766 {
/**
* 1 ~ n 까지 문제(숫자가 작을 수록 쉬운 문제)
* 1. N개의 문제 모두 풀어야함.
* 2. 먼저 푸는 것이 좋은 문제부터 풀어야함
* 3. 가능한 쉬운 문제부터 풀어야함
*/
/**
* 4 2 // 문제 수, 문제 순서쌍 갯수
* 4 2 // 4가 2보다 먼저 풀면 좋은 문제 4 -> 2
* 3 1 // 3이 1보다 먼저 풀면 좋은 문제 3 -> 1
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 문제 수
int n = Integer.parseInt(st.nextToken());
// 문제 순서쌍 갯수
int m = Integer.parseInt(st.nextToken());
// 인접 리스트
List<Integer>[] list = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
// 진입 차수 배열
int[] inDegree = new int[n+1];
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
list[node1].add(node2);
inDegree[node2]++;
}
// 가능한 쉬운 문제 부터 풀어야하기 때문에 우선순위 큐 사용(오름 차순)
Queue<Integer> queue = new PriorityQueue<>();
for(int i = 1; i <= n; i++) {
// 노드의 인접 차수가 0인 노드를 큐에 삽입
if(inDegree[i] == 0) {
queue.offer(i);
}
}
// 위상 정렬 배열
int[] result = new int[n+1];
StringBuilder sb = new StringBuilder();
while(!queue.isEmpty()) {
Integer node = queue.poll();
// 위상 정렬 배열에 노드를 삽입
result[node] = node;
sb.append(node).append(" ");
for(Integer i : list[node]) {
// 노드의 인접 노드의 인접 차수를 1 감소
inDegree[i]--;
// 인접 차수가 0이면
if(inDegree[i] == 0) {
// 큐에 삽입
queue.offer(i);
}
}
}
System.out.print(sb);
br.close();
}
}백준 1516
문제가 잘 이해가되지 않아서 혼자 해결하지 못했습니다..
입력
// 건물은 동시에 지을 수 있다.
5 // 건물 종류 수
10 -1 // 1번 건물 짓는데 걸리는 시간(10)
10 1 -1 // 2번 건물 짓는데 걸리는 시간(10), 건물 번호(1)부터 먼저 지어야함
4 1 -1 // 3번 건물 짓는데 걸리는 시간(4), 건물 번호(1)부터 먼저
4 3 1 -1 // 4번 건물 짓는데 걸리는 시간(4), 건물 번호(3, 1)먼저
3 3 -1 // 5번 건물 짓는데 걸리는 시간(3), 건물 번호(3) 먼저이 문제에서 중요한 부분은
건물을 지을 때마다 그 건물을 짓기 전까지 걸린 누적 시간(result)을 모두 구해주고,
마지막에 출력할 때 특정 건물 자신을 짓는 데 걸린 시간(time)과 result를 더하면(time + result) 됩니다.
// 특정 건물을 짓기 전까지 걸린 시간
int[] result = new int[n+1];
while (!queue.isEmpty()) {
Integer node = queue.poll();
// i 건물을 짓기위해서는 node 건물을 먼저 지어야 한다.
for(Integer i : list[node]) {
// 노드의 인접 노드의 인접 차수를 1 감소
inDegree[i]--;
// 인접 노드(i)의 건물을 짓기 전 노드(node)의 건물을 짓는데 걸린시간 중 최댓값
result[i] = Math.max(result[i], result[node] + times[node]);
if(inDegree[i] == 0) {
queue.offer(i);
}
}
}
StringBuilder sb = new StringBuilder();
// 특정 건물을 짓는 데 걸린 시간을 출력.
for (int i = 1; i <= n; i++) {
sb.append((result[i] + times[i]) + "\n");
}
풀이
public class Quiz1516 {
/**
* 건물은 동시에 지을 수 있다.
*
* 5 // 건물 종류 수
* 10 -1 // 1번 건물 짓는데 걸리는 시간(10)
* 10 1 -1 // 2번 건물 짓는데 걸리는 시간(10), 건물 번호(1)부터 먼저 지어야함
* 4 1 -1 // 3번 건물 짓는데 걸리는 시간(4), 건물 번호(1)부터 먼저
* 4 3 1 -1 // 4번 건물 짓는데 걸리는 시간(4), 건물 번호(3, 1)먼저
* 3 3 -1 // 5번 건물 짓는데 걸리는 시간(3), 건물 번호(3) 먼저
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 건물 종류 수
int n = Integer.parseInt(br.readLine());
// 인접 리스트
List<Integer>[] list = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
// 진입 차수(특정 건물을 짓기 전에 먼저 지어야할 건물의 갯수)
int[] inDegree = new int[n+1];
// 걸리는 시간(특정 건물을 짓는데 걸리는 시간)
int[] times = new int[n+1];
for(int i = 1; i <= n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
times[i] = Integer.parseInt(st.nextToken());
while (true) {
int building = Integer.parseInt(st.nextToken());
if(building == -1) {
break;
}
// building -> i번 건물(building을 지어야 i번째 건물 짓기 가능)
list[building].add(i);
inDegree[i]++;
}
}
Queue<Integer> queue = new ArrayDeque<>();
for(int i = 1; i <= n; i++) {
if(inDegree[i] == 0) {
queue.offer(i);
}
}
// 특정 건물을 짓기 전까지 걸린 시간
int[] result = new int[n+1];
while (!queue.isEmpty()) {
Integer node = queue.poll();
// i 건물을 짓기위해서는 node 건물을 먼저 지어야 한다.
for(Integer i : list[node]) {
// 노드의 인접 노드의 인접 차수를 1 감소
inDegree[i]--;
// 인접 노드(i)의 건물을 짓기 전 노드(node)의 건물을 짓는데 걸린시간 중 최댓값
result[i] = Math.max(result[i], result[node] + times[node]);
if(inDegree[i] == 0) {
queue.offer(i);
}
}
}
StringBuilder sb = new StringBuilder();
// 특정 건물을 짓는 데 걸린 시간을 출력.
for (int i = 1; i <= n; i++) {
sb.append((result[i] + times[i]) + "\n");
}
System.out.print(sb);
}
}백준 1005
백준 1516와 동일한 문제 입니다.
마찬가지로 이 문제에서 중요한 부분은
건물을 지을 때마다 그 건물을 짓기 전까지 걸린 누적 시간(result)을 모두 구해주고,
마지막에 출력할 때 특정 건물 자신을 짓는 데 걸린 시간(time)과 result를 더하면(time + result) 됩니다.
풀이
public class Quiz1005 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 테스트 케이스
int t = Integer.parseInt(br.readLine());
for(int tc = 0; tc < t; tc++) {
StringTokenizer st = new StringTokenizer(br.readLine());
// 건물 갯수
int n = Integer.parseInt(st.nextToken());
// 건설 규칙 수
int k = Integer.parseInt(st.nextToken());
// 건물 짓는 시간
int[] times = new int[n+1];
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= n; i++) {
times[i] = Integer.parseInt(st.nextToken());
}
// 인접 리스트 초기화
List<Integer>[] list = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
// 진입 차수 배열
int[] inDegree = new int[n+1];
// 건설 순서(node1 -> node2)
for(int i = 0; i < k; i++) {
st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
// node1 -> node2
list[node1].add(node2);
// 인접 노드의 진입 차수 증가
inDegree[node2]++;
}
// 승리하기 위해 지어야하는 건물
int finalBuilding = Integer.parseInt(br.readLine());
// 특정 건물을 짓기 전까지 걸린 시간
int[] result = new int[n+1];
// 위상 정렬
topologicalSort(n, times, list, inDegree, result);
System.out.println(times[finalBuilding] + result[finalBuilding]);
}
br.close();
}
private static void topologicalSort(int n, int[] times, List<Integer>[] list, int[] inDegree, int[] result) {
Queue<Integer> queue = new ArrayDeque<>();
for(int i = 1; i <= n; i++) {
// 진입 차수가 0 이면
if(inDegree[i] == 0) {
// 큐에 노드 삽입
queue.offer(i);
}
}
while (!queue.isEmpty()) {
Integer node = queue.poll();
for(Integer i : list[node]) {
// 진입 차수 감소
inDegree[i]--;
// 특정 건물을 짓기전 걸린시간 계산
result[i] = Math.max(result[i], result[node] + times[node]);
// 진입 차수가 0 이면
if(inDegree[i] == 0) {
// 큐에 노드 삽입
queue.add(i);
}
}
}
}
}
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 벨만-포드(백준 11657, 1865, 1219 -Java) (0) | 2023.04.05 |
|---|---|
| [알고리즘] 다익스트라(백준 1238, 1753, 1916, 4485 -Java) (1) | 2023.04.02 |
| [알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java) (1) | 2023.03.29 |
| [알고리즘] 이분 그래프(백준 1707, 1953, 12893 -Java) (0) | 2023.03.25 |
| [알고리즘] 그래프 기본 개념 찍먹하기 -Java (2) | 2023.03.25 |
