[알고리즘] 그래프 기본 개념 찍먹하기
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
그래프의 개념과 그래프 개념을 사용하는 알고리즘 종류에 대해서 간단하게 알아보자!

그래프
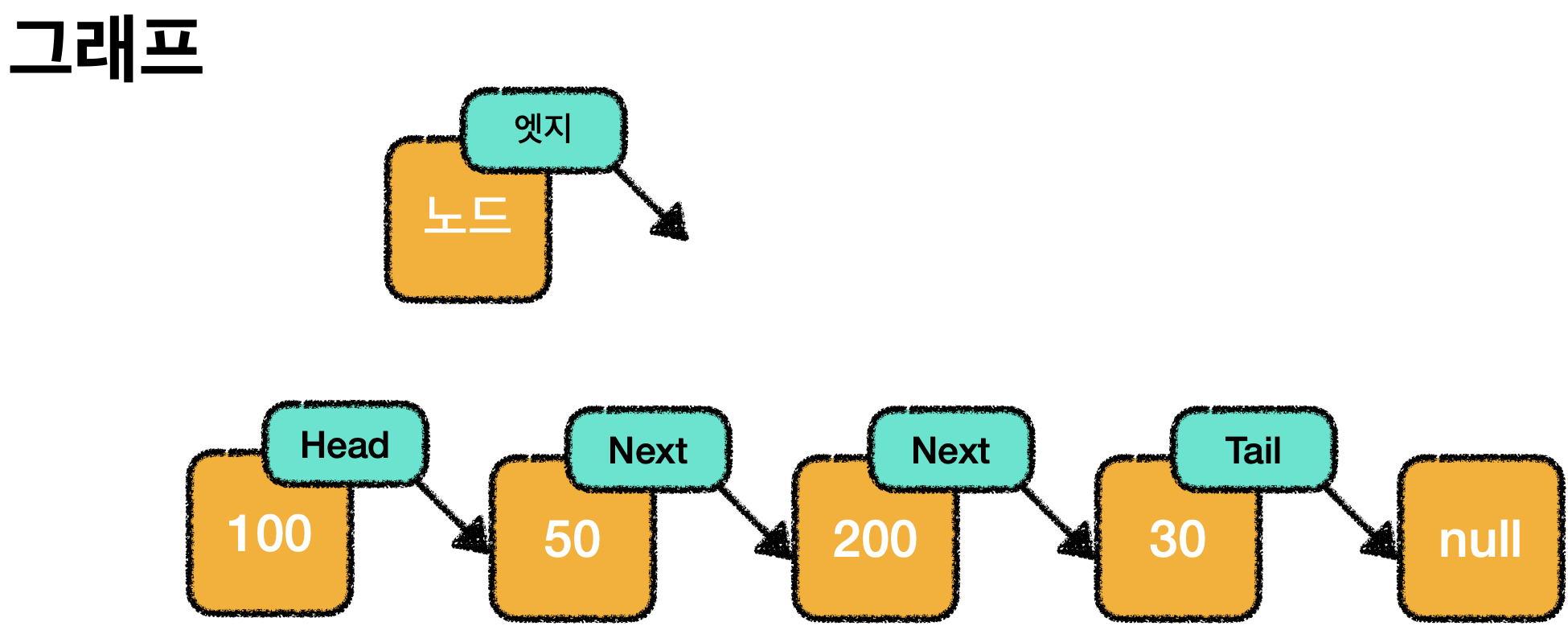
알고리즘에서 그래프는 노드와 엣지로 구성된 집합 입니다.
노드는 데이터를 표현하는 단위이고, 엣지는 노드를 연결합니다.
그래프를 구현하는 방법
- 엣지 리스트
- 가중치가 없는 경우
- 가중치가 있는 경우
- 인접 행렬
- 가중치가 없는 경우
- 가중치가 있는 경우
- 인접 리스트
- 가중치가 없는 경우
- 가중치가 있는 경우
엣지 리스트
엣지 리스트는 엣지를 중심으로 그래프를 표현 합니다.
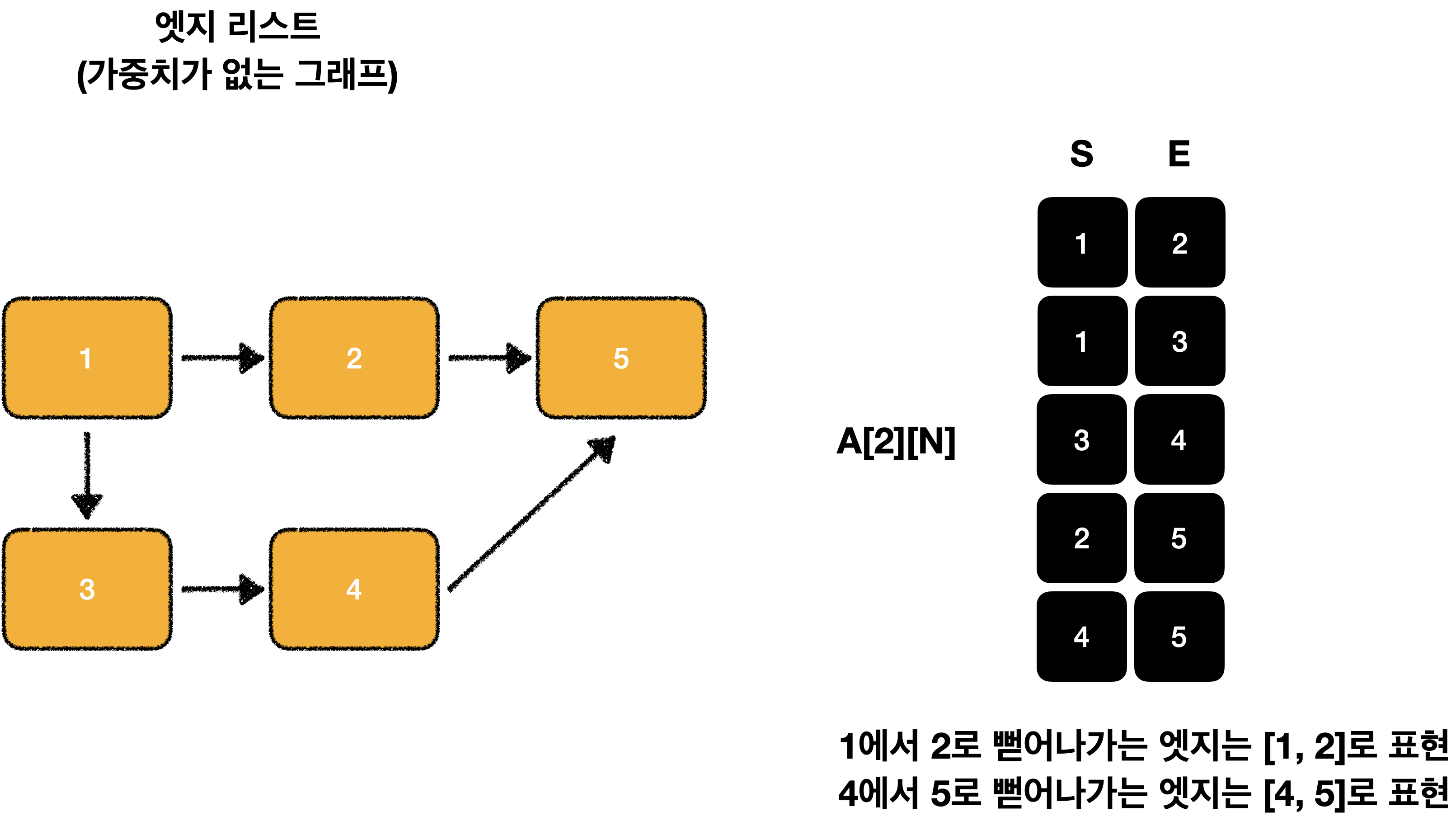
엣지 리스트로 가중치 없는 그래프 표현하기
가중치가 없는 그래프는 출발 노드와 도착 노드만 표현하기 때문에 배열의 행은 2개면 충분 합니다.
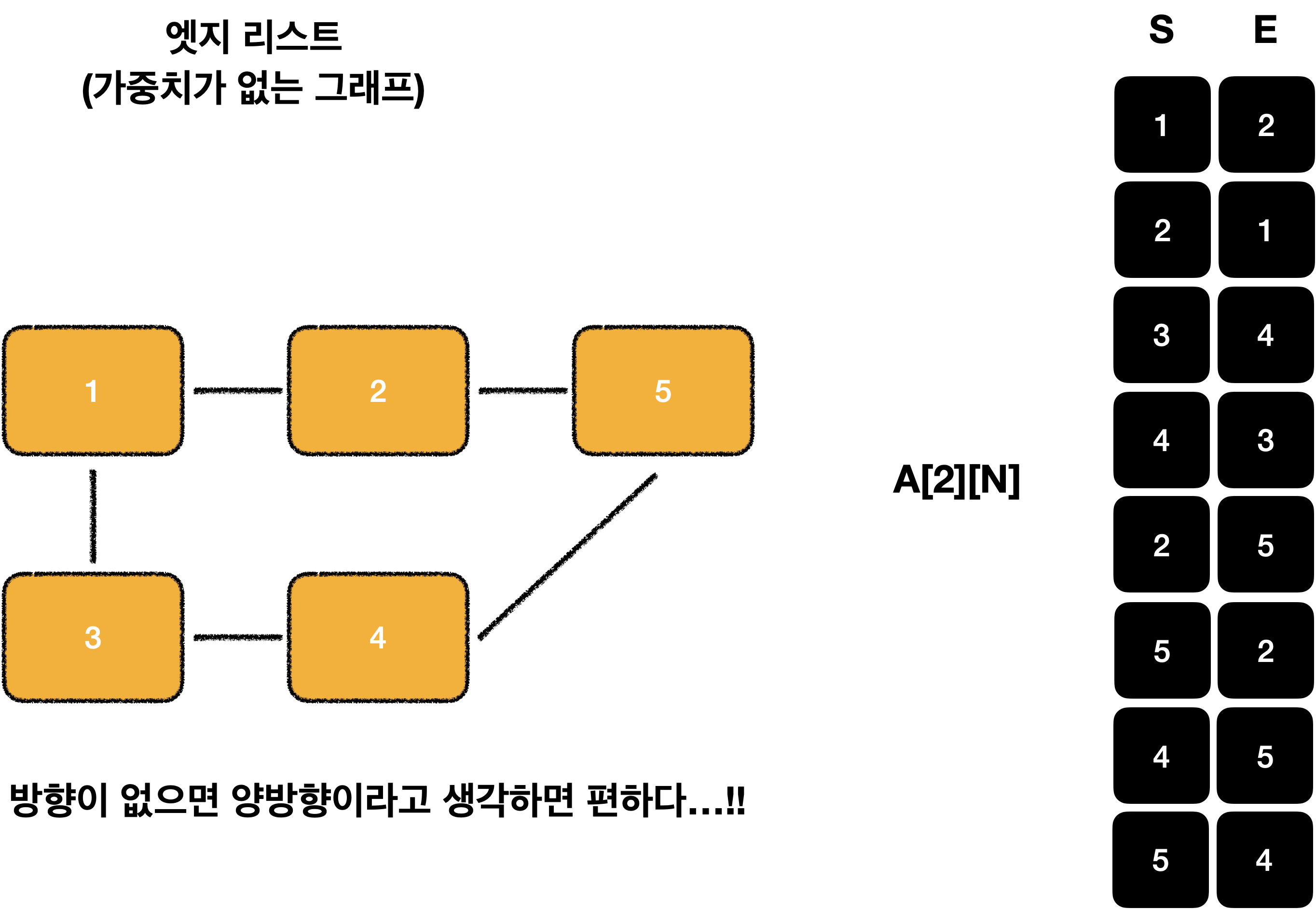
만약 방향이 없다면? 🤔
그렇다면 가중치가 있으면? 🤔
엣지 리스트로 가중치 있는 그래프 표현하기
간단하다 가중치까지 저장하면 된다!
(노드 중심 알고리즘에는 잘 사용하지 않습니다.)

예를 들어 2번 노드에서 출발하는 엣지를 검색하고 싶으면,
배열을 완전 탐색해야합니다. 따라서 시간이 많이 걸리게 됩니다.
인접 행렬
인접 행렬은 2차원 배열을 자료구조로 활용하여 그래프를 표현합니다.
인접 행렬은 엣지 리스트와 다르게 노드 중심으로 그래프를 표현 합니다.
e.g) 노드가 5개인 그래프를 5 x 5 인접 행렬로 표현 합니다.
노드 중심으로 표현한다라는 말은
인덱스를 이용해서 시작노드, 노착노드를 표현 한다는 의미 입니다.
인접 행렬로 가중치 없는 그래프 표현
인덱스를 이용해서 시작노드, 노착노드를 표현 합니다.
노드A에서 노드B로 향하는 에지를 1로 저장합니다.
향하는 엣지가 없으면 0을 저장합니다.

그렇다면 가중치가 있으면? 🤔
인접 행렬로 가중치 있는 그래프 표현
생각보다 간단합니다.!노드A에서 노드B로 향하는 에지를 가중치로 저장합니다.
향하는 엣지의 가중치가 없으면 0을 저장합니다.

이처럼 인접 행렬을 이용한 그래프 구현은 생각보다 간단 합니다. 👍
두 노드를 연결하는 엣지의 여부와 가중치 값은 배열에 직접 접근하면 바로 확인할 수 있는 것도 장점 입니다.
하지만, 노드와 관련되어 있는 엣지를 탐색하려면 N번 접근해야 합니다. 😭
(예를 들어 2번 노드의 엣지를 탐색한다고 해보자. 그러면 A[2][N], N번을 탐색해야 합니다.)
노드 갯수에 비해 엣지가 적을때는 공간 효율성이 떨어집니다.
(시간 복잡도, 공간 복잡도 안 좋음)
또한, 노드 갯수가 많은 경우 2차원 배열 선언 자체를 할 수 없는 경우도 발생합니다.
(노드가 3만개가 넘어가면 JavaHeapSpace 에러가 발생)
따라서 인접 행렬은 노드 갯수에 따라 사용 여부를 적절하게 판단하는 능력도 필요합니다.
인접 리스트
인접 행렬이 편하다는 것을 느꼈을 것 입니다.
그런데 노드의 갯수가 너무 많으면 사용할 수 없습니다….
이러한 단점을 극복하기 위해서 리스트(List)를 사용하면 됩니다.!
인접 리스트는 ArrayList로 그래프를 표현 합니다.
노드 갯수만큼 ArrayList를 선언 합니다.
// 가중치가 없는 그래프 표현
List<Ingteger>[N] list1 = new ArrayList[N];
// 가중치가 있는 그래프 표현
List<Node> list2 = new ArrayList<>();인접 리스트 가중치 없는 그래프 표현
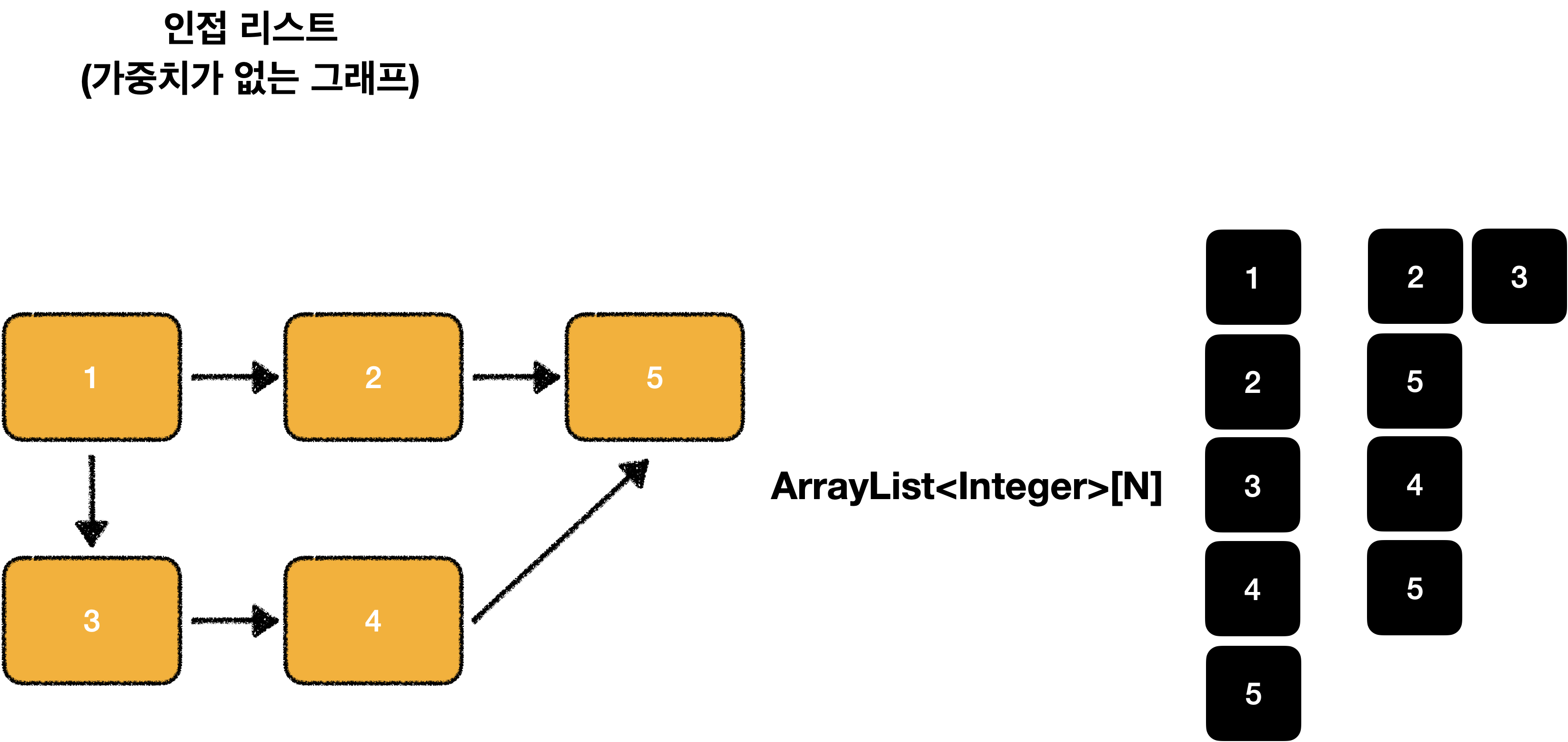
예를 들어 노드 1과 연결과 연결된 노드 2, 3은 ArrayList[1]에 [2, 3]을 연결하는 방식으로 표현 합니다.
인접 리스트 가중치 있는 그래프 표현

ArrayList[1]에 [(2, 8), (3, 3)]이 연결되어 있습니다.
이는 노드 1과 2가 가중치 8 엣지로, 1과 3이 가중치 3 엣지로 연결되어 있다는 것을 의미 합니다.
참고Node를 엣지와 가중치를 포함하는 클래스를 생성하여 활용 합니다.
public class Node {
private int n;
private int v;
public Node(int n, int v) {
this.n = n;
this.v = v;
}
}
그래프를 사용하는 알고리즘의 종류는 다음과 같습니다.
- 유니온 파인드
- 위상 정렬
- 다익스트라(최단 거리 알고리즘)
- 벨만-포드(최단 거리 알고리즘)
- 플로이드-워셜(최단 거리 알고리즘)
- 최소 신장 트리
그래프를 사용하는 알고리즘은 어떤 것인지 간단하게 찍먹 해봅시다.^^
유니온 파인드
그래프의 사이클이 생성 되는지 판별하는 알고리즘 입니다.
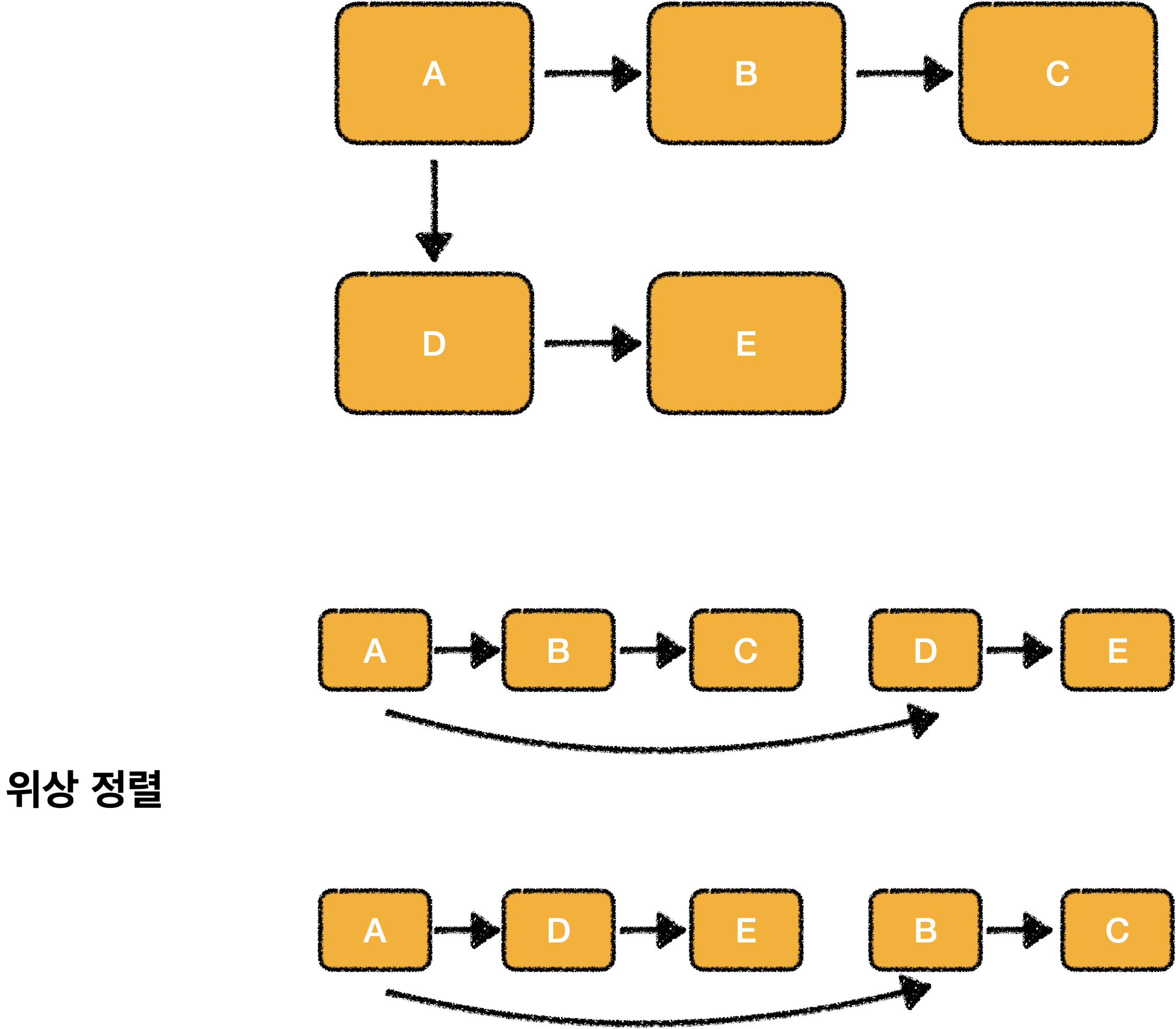
위상 정렬
사이클이 없고, 방향이 있는 그래프에서 그래프의 노드를 선형으로 정렬하는 것
위상 정렬 했을 때 값은 일정하지 않습니다.
위상 정렬을 활용하는 예로 대학교 선수 과목을 예로 들 수 있습니다.C과목을 들으려면 B과목을 들어야하고 B과목을 들으려면 A과목을 들어야 하죠
다익스트라
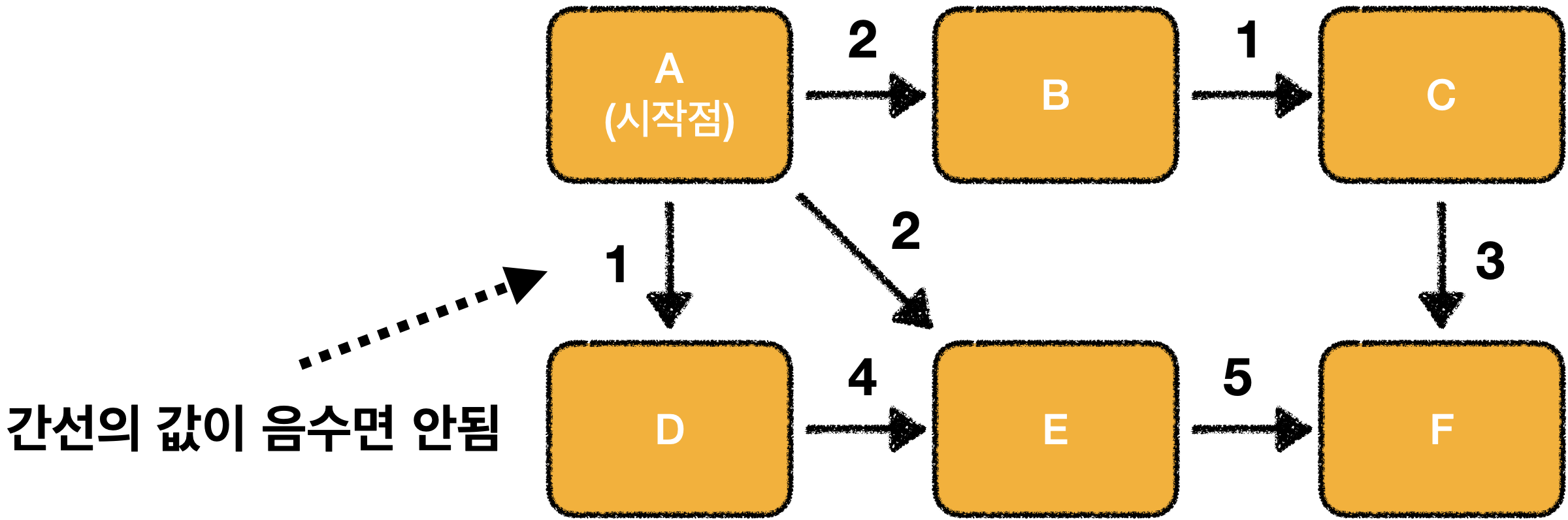
시작점이 있고 다른 모든 노드로 가는 최단거리를 구하는 알고리즘 입니다.
(단, 음수 간선은 존재하면 안됨)
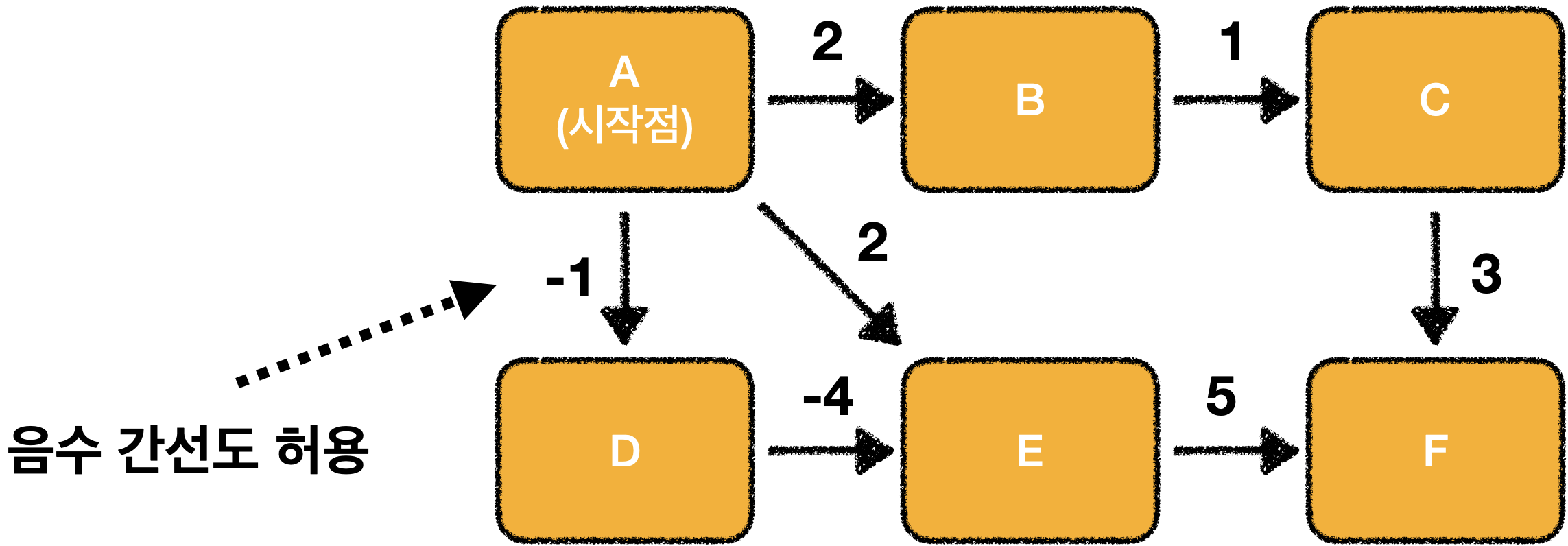
벨만-포드
벨만 포드는 다익스트라와 개념은 동일한데, 음수 간선도 허용 합니다.
(엣지를 기준으로 알고리즘을 활용합니다.)
최단거리를 구하는 문제보다는
음수 사이클이 존재하는지에 대한 문제가 자주 출제 됩니다.
플로이드-워셜
모든 노드에 대해서 최단거리를 구하는 알고리즘 입니다.
(단, 다익스트라, 벨만-포드에 비하여 시간복잡도가 안 좋습니다.)
최단거리를 알고 싶은 노드 2개를 선택하면 됩니다.
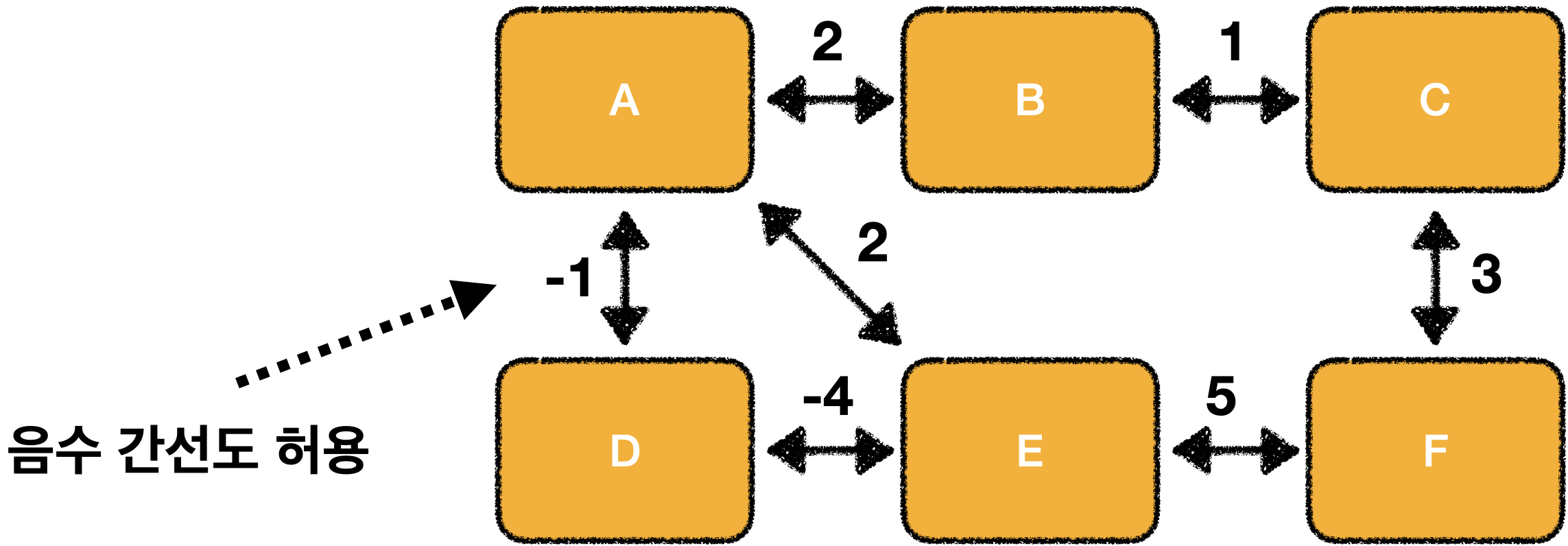
최소 신장 트리
모든 노드를 연결하는데 발생하는 간선의 비용을 최소로 만드는 알고리즘
사이클이 있으면 안되기 때문에 유니온 파인드를 이용하여 사이클 생성 여부를 확인 합니다.
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 유니온 파인드(백준 1717, 1976, 1043, 4195, 20040 -Java) (0) | 2023.03.29 |
|---|---|
| [알고리즘] 이분 그래프(백준 1707, 1953, 12893 -Java) (0) | 2023.03.25 |
| [알고리즘] 그리디 알고리즘(백준 11047, 1541, 11399, 1931, 1026 -Java) (0) | 2023.03.24 |
| [알고리즘] 이진 탐색(백준 1920, 10815, 10816, 1654, 2805, 2110 -Java) (0) | 2023.03.24 |
| [알고리즘] 너비 우선 탐색(BFS: Breadth First Search, 백준 2178, 1697, 12851, 1012 -Java) (0) | 2023.03.19 |