[알고리즘] 플로이드-워셜(백준 11404, 1389, 11403 -Java)
알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇
본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
물론 혼자하면 작심삼일이 될거 같아
무료 Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
강의 커리큘럼에 맞춰 공부해보자!!
[무료] Do it! 알고리즘 코딩테스트 with JAVA - 인프런 | 강의
IT기업 코딩테스트 대비를 위한 [자료구조 및 알고리즘 핵심이론 & 관련 실전 문제 풀이 강의] 입니다. - JAVA 편 -, - 강의 소개 | 인프런
www.inflearn.com
플로이드-워셜
플로이드-워셜 알고리즘은 방향 그래프에서 최단 거리를 구하는 알고리즘 입니다.
다익스트라, 벨만-포드와 다른 점은 동적 계획법(DP)의 원리를 이용해서 모든 노드 간에 최단 경로를 탐색 할 수 있습니다.
시간 복잡도는 O(V^3) 입니다.(V: 노드의 수)
(코딩 테스트에서 V가 1,000정도 되면 사용할 수 없다.)
참고
- 다익스트라
- 특정 노드(
출발 노드)에서 모든 노드 까지의 최단거리를 구할 수 있는 알고리즘(방향 그래프) - 가중치가 양수 일때만 사용 가능
- 사이클이 없어야 함(양방향 안됨)
- 사이클 유무는
유니온-파인드를 통해 확인 가능
- 사이클 유무는
- 특정 노드(
- 벨만-포드
- 특정 노드(
출발 노드)에서 모든 노드 까지의 최단거리를 구할 수 있는 알고리즘(방향 그래프) - 가중치가 음수, 양수 일때 사용 가능
- 음수 사이클 발생 여부를 판단할 수 있음
- 음수 사이클이 발생하면 최단 거리가 무의미함
- 특정 노드(
플로이드-워셜 핵심 이론
플로이드-워셜 알고리즘의 핵심 원리는 A노드에서 B노드까지 최단 경로를 구했다고 가정했을 때
최단 경로 위에 K노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로라는 것 입니다.
말이 좀 어려운데 그림으로 설명하면 다음과 같습니다.
즉, 최단 경로를 이어 붙이면 최단 경로가 나온다는 말 입니다.

현재 s -> e 로 가는 최단 거리와 s- -> k -> e 로 가는 경로(경유지를 거친 경로) 를 비교하여
작은 값을 최단 거리로 갱신하는 방법 입니다.
이를 수식으로 표현하면 다음과 같습니다.
s: 시작 노드, e: 도착 노드, k: 중간 노드
D[s][e] = Math.min(D[s][e], D[s][k] + D[k][e])
그럼 한번 플로이드-워셜을 사용해봅시다.
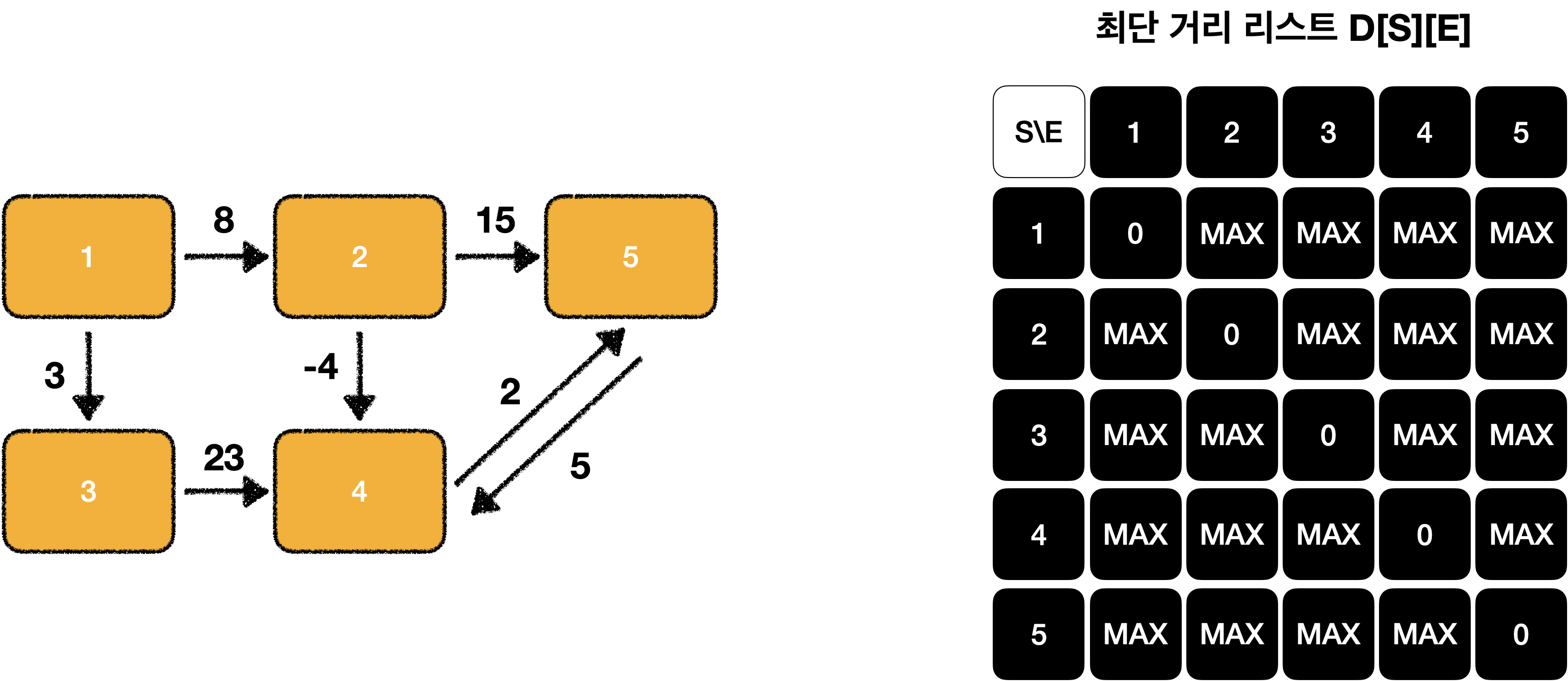
먼저 아래와 같은 그래프가 있을 때 D[s][e]를 표현해야 합니다.s와 e가 같으면 자기 자신의 거리이기 때문에 0으로 초기화하고,
다른 칸은 거리를 모르기 때문에 MAX로 초기화 합니다.
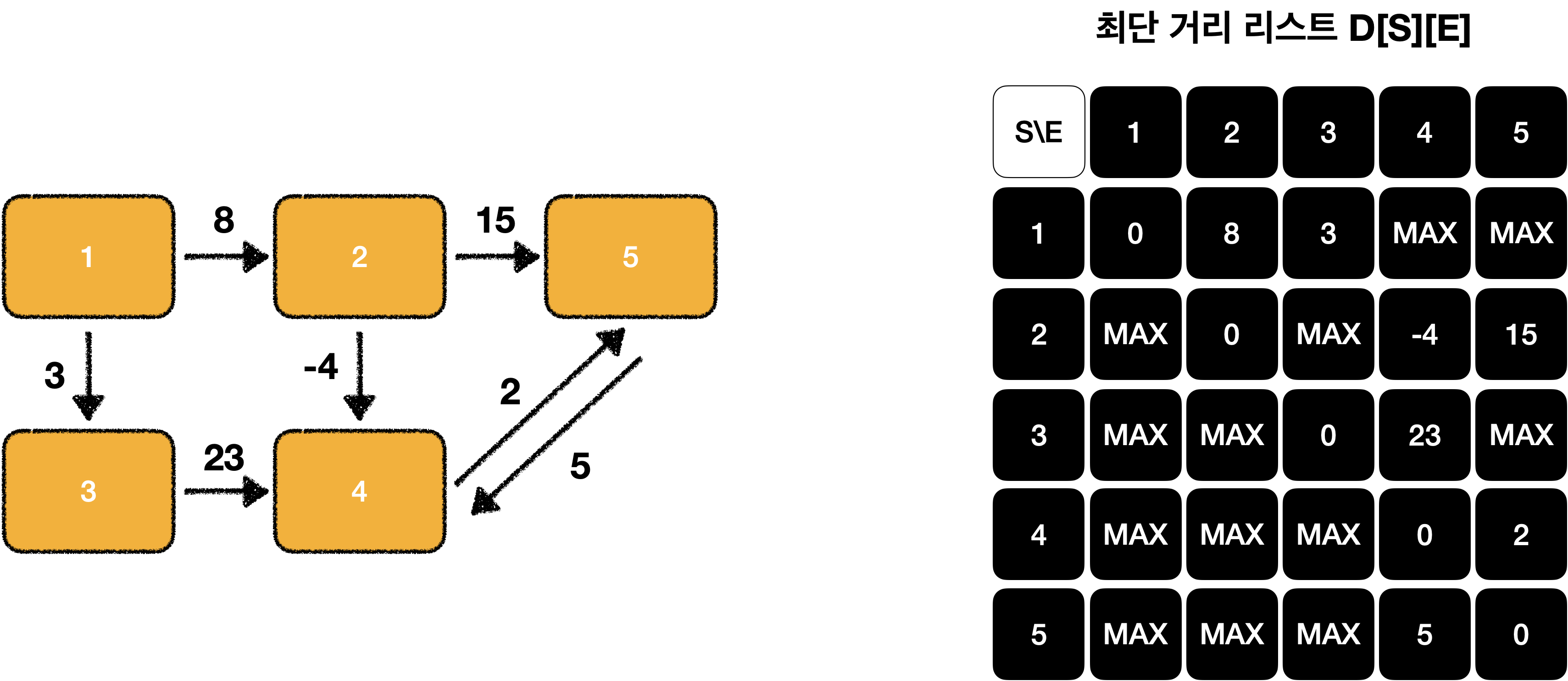
그다음에 가중치를 D[s][e]에 반영 합니다.
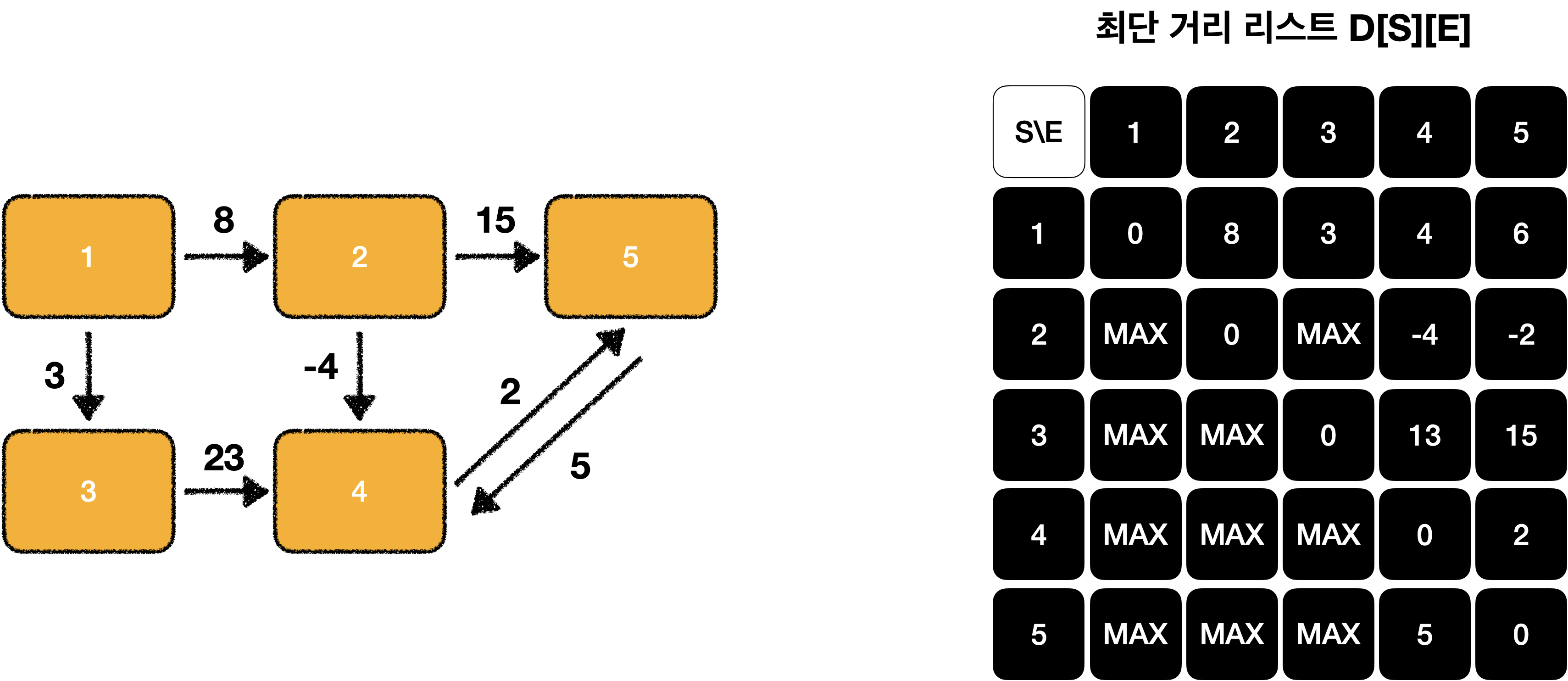
이제 이걸 반복합니다.
3중 loop를 사용합니다.
for 경유지 k에 대해
for 출발 노드 s에 대해
for 도착 노드 e에 대해
D[s][e] = Math.min(D[s][e], D[s][k] + D[k][e])
현재 s -> e 로 가는 최단 거리(D[s][e])와
s- -> k -> e 로 가는 경로(D[k][e])를 비교하여
작은 값을 최단 거리로 갱신
결과
어 그러면 최단경로 문제를 플로이드-워셜만 사용하면 되네? 🤔
3중 loop를 사용하기 때문에 코딩 테스트에서 V가 1,000정도 되면 사용할 수 없습니다.😭
자 이제 문제를 풀어봅시다.^^
백준 11404
문제에서 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
라는 것을 간과하여 조금 애먹었습니다….
(문제를 잘 읽읍시다…)
그리고 플로이드-워셜을 사용할 때 overFlow를 주의 하셔야 합니다.
D[s][e] = Math.min(D[s][e], D[s][k] + D[k][e])을 연산할 때
D[s][k] + D[k][e] 과정에서 overFlow가 발생할 수 있기 때문에
적절한 값으로 D[n][n]을 초기화 해야합니다.
e.g) 987654321
풀이
public class Quiz11404 {
// overFlow 주의
static int INF = 987654321;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 도시 갯수
int n = Integer.parseInt(br.readLine());
// 버스 갯수
int m = Integer.parseInt(br.readLine());
// 최단 거리 저장 배열
long[][] result = new long[n+1][n+1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <=n; j++) {
if(i == j) result[i][j] = 0;
else result[i][j] = INF;
}
}
for(int i = 0; i < m; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
// 비용이 저렴한 것으로 저장한다.
result[start][end] = Math.min(result[start][end], weight);
}
// 플로이드 워셜 수행
for(int k = 1; k <= n; k++) {
for (int s = 1; s <= n; s++) {
for (int e = 1; e <= n; e++) {
// result[s][k] + result[k][e] 연산시 overFlow 주의!
result[s][e] = Math.min(result[s][e], result[s][k] + result[k][e]);
}
}
}
StringBuilder sb = new StringBuilder();
for(int i = 1; i <= n; i++) {
for(int j = 1; j <=n; j++) {
// i에서 j로 가지 못하는 경우 INF 이기 때문에 0을 출력
if(result[i][j] == INF) sb.append(0).append(" ");
else {
sb.append(result[i][j]).append(" ");
}
}
sb.append("\n");
}
System.out.print(sb);
br.close();
}
}백준 11403
처음에 유니온-파인드를 이용해서 문제를 해결하려고 했습니다.
하지만, 위 문제에서는 방향이 있는 그래프 였습니다..
유니온-파인드는 방향이 없는 그래프에서만 사용할 수 있습니다.!!
따라서 플로이드-워셜 알고리즘을 사용해서 해결했습니다.
풀이
public class Quiz11403 {
// overFlow 주의
static int INF = 987654321;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 정점 갯수
int n = Integer.parseInt(br.readLine());
// 최단 거리 인접 행렬 초기화
int[][] map = new int[n][n];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
map[i][j] = INF;
}
}
// 그래프 생성
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 0; j < n; j++) {
int road = Integer.parseInt(st.nextToken());
if(road == 1) {
map[i][j] = road;
}
}
}
// 플로이드 워셜 수행
for(int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
map[i][j] = Math.min(map[i][j], map[i][k] + map[k][j]);
}
}
}
StringBuilder sb = new StringBuilder();
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
int value = map[i][j];
if(value == INF) sb.append(0).append(" ");
else sb.append(1).append(" ");
}
sb.append("\n");
}
System.out.println(sb);
br.close();
}
}백준 1389
플로이드-워셜을 사용하여 문제를 해결했습니다.
코드에 주석을 보면 이해하실 수 있을 것 입니다.^^
풀이
public class Quiz1389 {
static int INF = 987654321;
// 모든 노드의 최단 거리를 구하면 된다.
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 친구 숫자
int n = Integer.parseInt(st.nextToken());
// 친구 관계 수
int m = Integer.parseInt(st.nextToken());
// 최단 거리 인접행렬 초기화
int[][] relation = new int[n+1][n+1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(i == j) relation[i][j] = 0;
else relation[i][j] = INF;
}
}
// 친구관계 그래프로 표현
for(int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int friend1 = Integer.parseInt(st.nextToken());
int friend2 = Integer.parseInt(st.nextToken());
// 친구 관계는 양방향
relation[friend1][friend2] = 1;
relation[friend2][friend1] = 1;
}
// 플로이드 워셜 수행
for(int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n ; j++) {
relation[i][j] = Math.min(relation[i][j], relation[i][k] + relation[k][j]);
}
}
}
// 케빈 베이컨 6단계 법칙 배열 초기화
List<Member> result = new ArrayList<>();
// 케빈 베이컨 6단계 법칙 계산
for(int i = 1; i <= n; i++) {
int sum = 0;
for(int j = 1; j <= n; j++) {
if(relation[i][j] != INF) {
sum += relation[i][j];
}
}
result.add(new Member(i, sum));
}
// 케빈 베이컨 수를 기준으로 오름차순 정렬
Collections.sort(result, (o1, o2) -> Integer.compare(o1.getSum(), o2.getSum()));
System.out.print(result.get(0).getNumber());
br.close();
}
static class Member {
private int number;
private int sum;
public Member(int number, int sum) {
this.number = number;
this.sum = sum;
}
public int getNumber() {
return number;
}
public int getSum() {
return sum;
}
}
}
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [백준 9205] 맥주 마시면서 걸어가기(Java) (0) | 2023.04.20 |
|---|---|
| [알고리즘] 이진 트리(백준 11725, 1911, 9934, 2263, 5639 -Java) (2) | 2023.04.12 |
| [알고리즘] 트리 기본 개념 (0) | 2023.04.12 |
| [알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386 -Java) (0) | 2023.04.10 |
| [알고리즘] 벨만-포드(백준 11657, 1865, 1219 -Java) (0) | 2023.04.05 |