[백준 1967] 트리의 지름(Java)
https://www.acmicpc.net/problem/1967
1967번: 트리의 지름
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연
www.acmicpc.net

해결 방법
결론
- 트리에서 노드 간의 최대 거리를 구할 때는 DFS를 이용한다.
- 루트 노드에서 가장 먼 노드를 찾는다.
- 아무 노드나 해도 상관 없음
- 찾은 노드에서 가장 먼 노드까지의 거리를 구한다.
1트
처음에는 엄청 쉽다고 생각했습니다. 😄
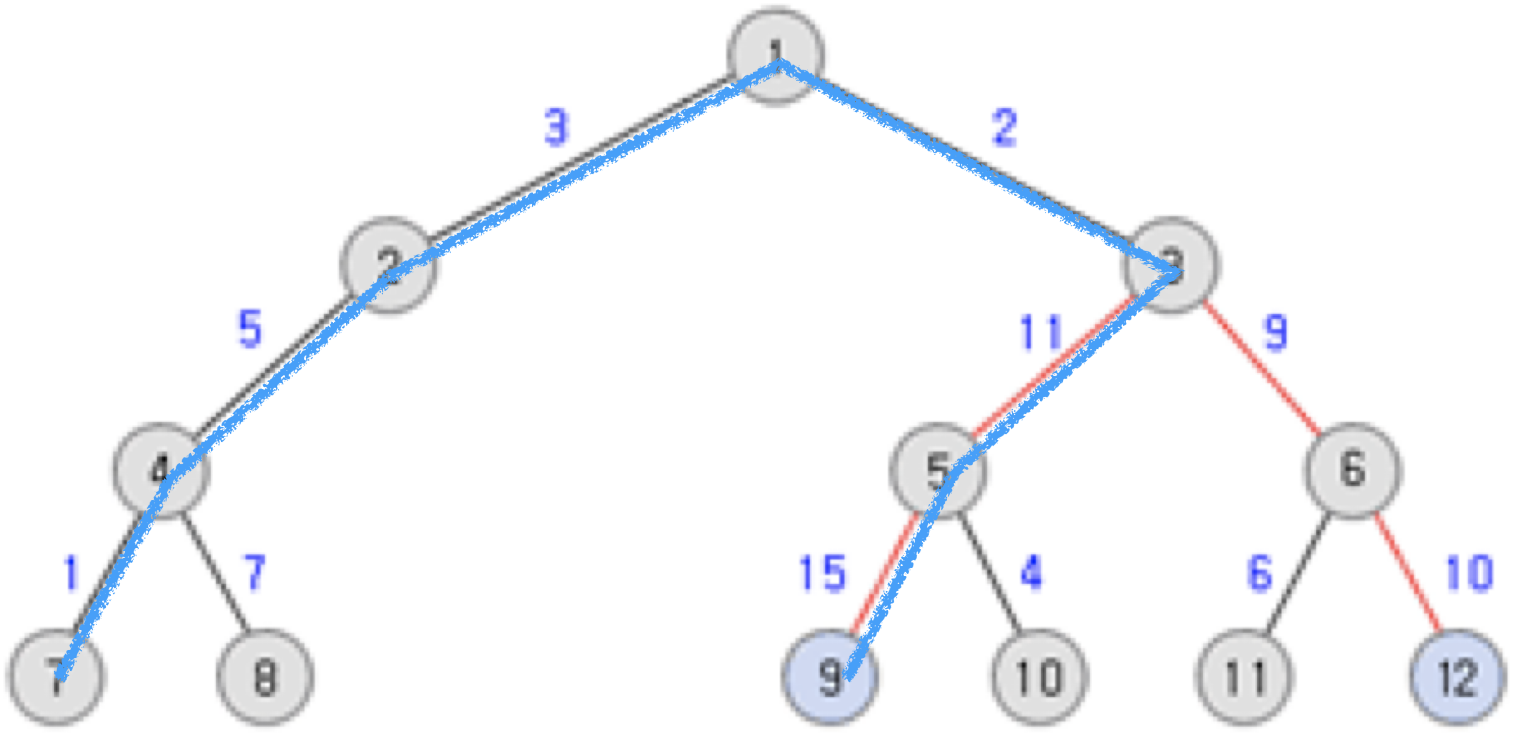
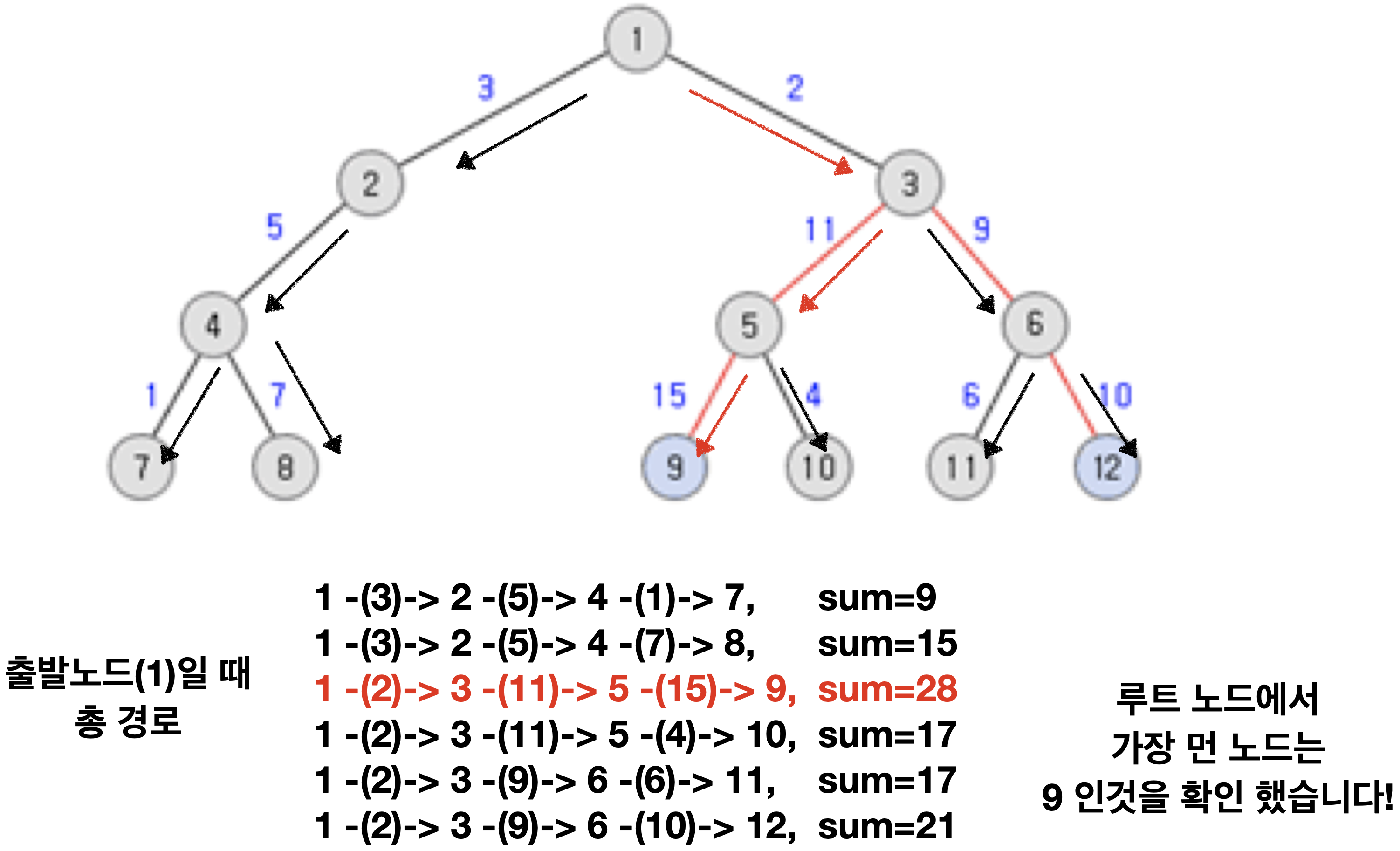
아 루트 노드를 중심으로 거리가 가장 먼 노드를 찾으면 되는구나!
라고 생각하여 계산해 보니 43이 나왔습니다…? 😲
정답은 45인데…
음.. 뭐지..?
2트(플로이드-워셜? DFS?)
도무지 이해가 안됐습니다.
그래서 문제를 뚫어져라 보니………….
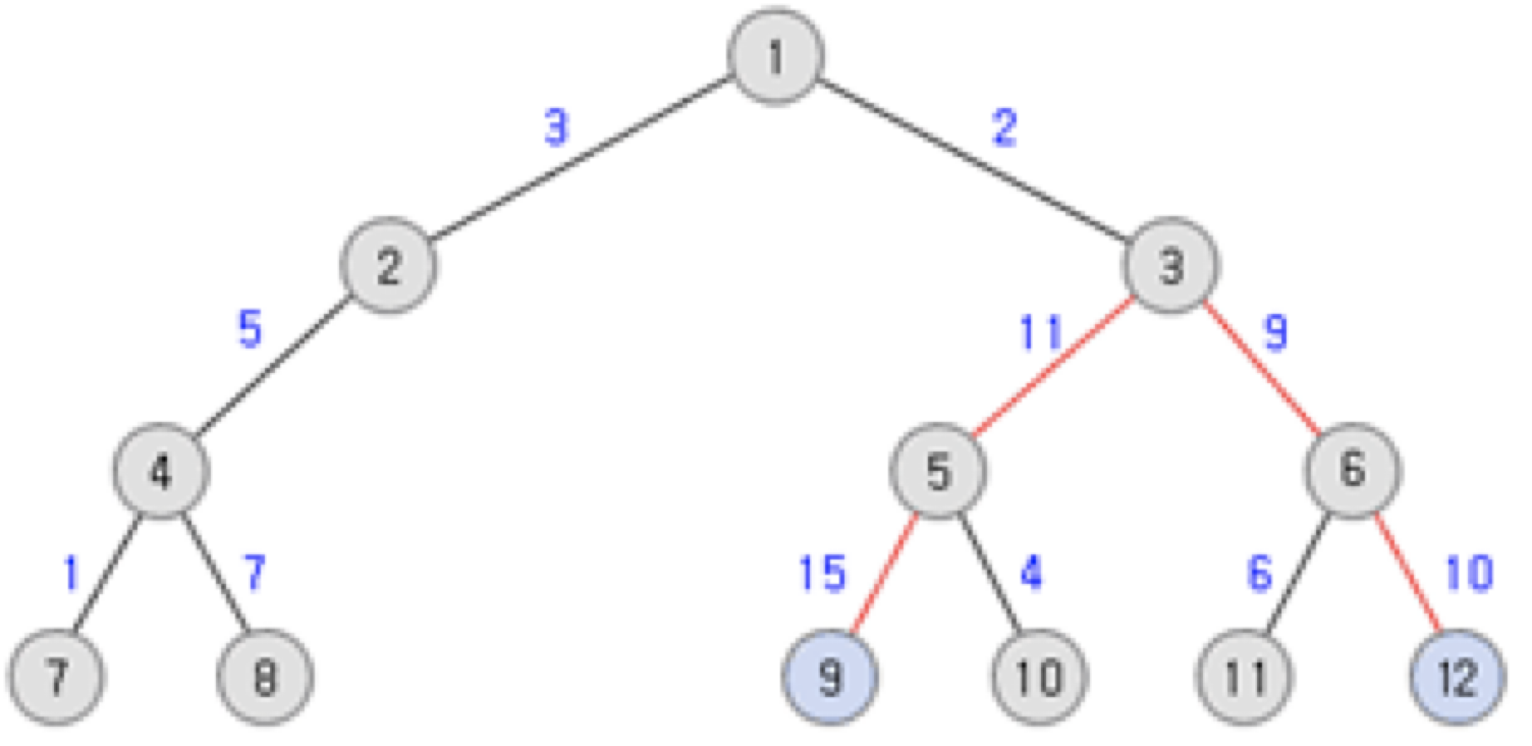
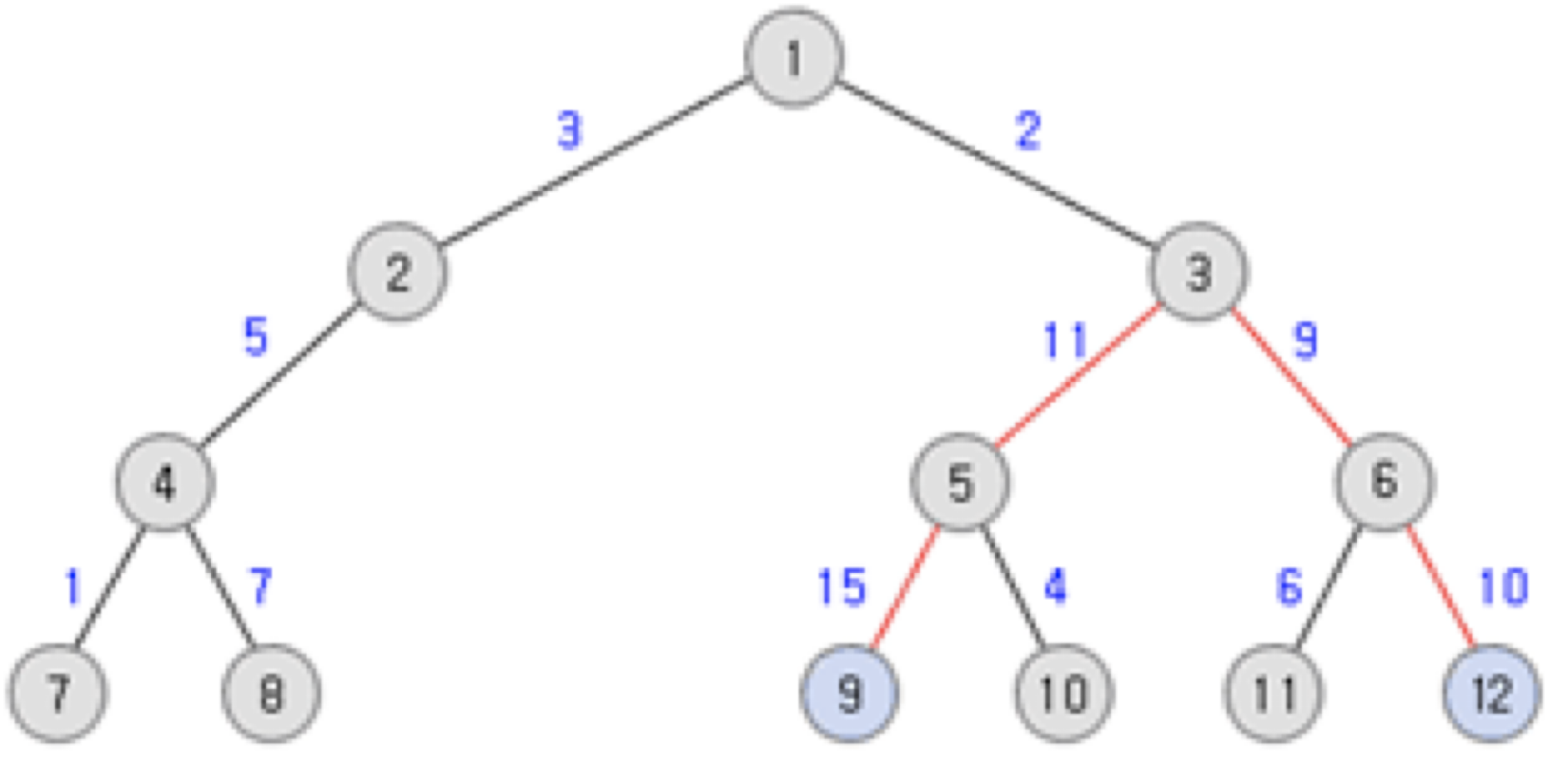
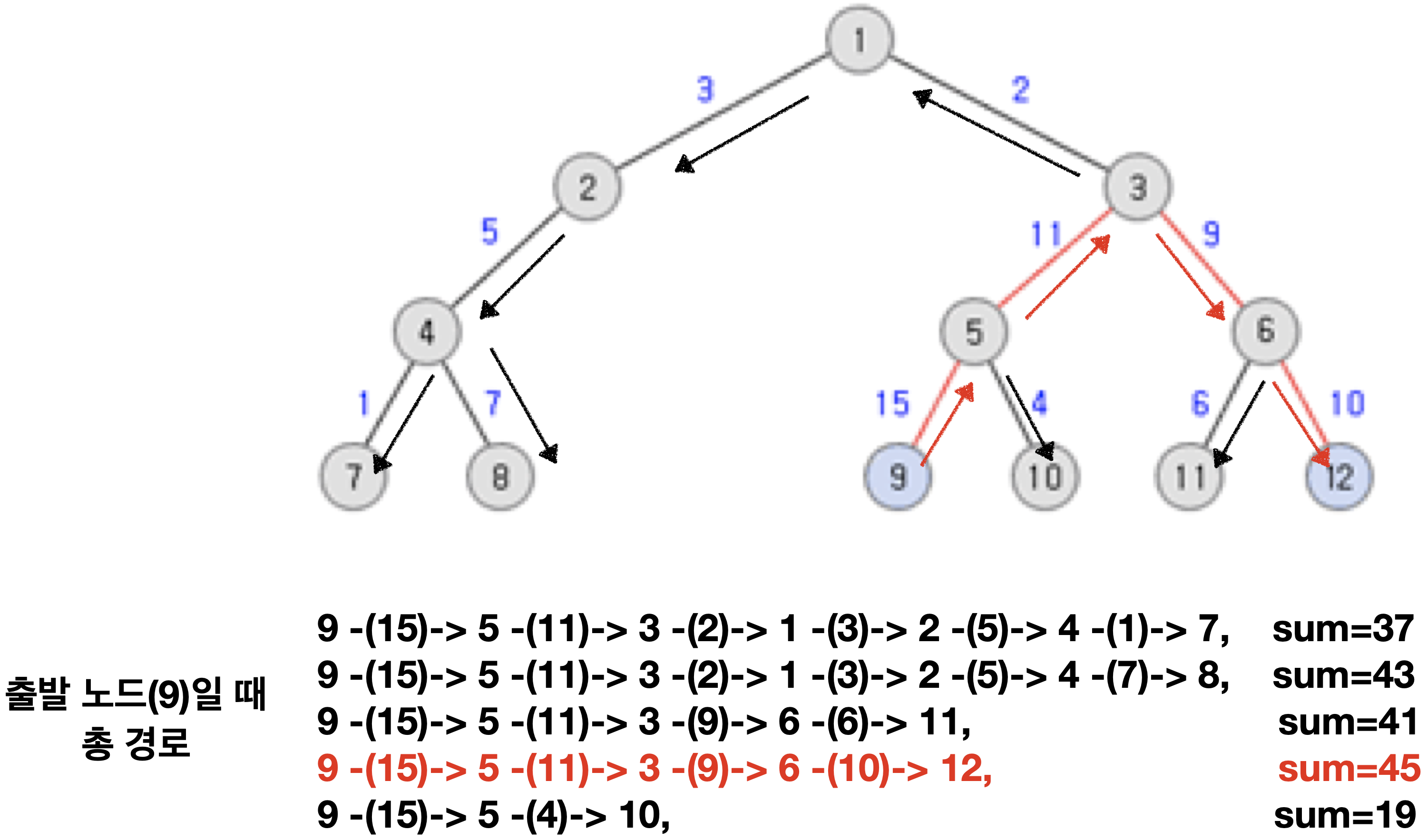
노드9 ~ 노드12까지의 거리가 최대 였습니다…!
오랜시간 고민한 결과 다음과 같은 생각을 했습니다.
1. 모든 노드에서 최대 거리를 구한다.
2. 1에서 나온 결과중 제일 큰 값을 출력
그래서
아 플로이드-워셜을 사용하면 되나?
라고 생각했습니다.
그런데 문제에서 n이 최대 10,000이라서 사용하면 안된다는 것을 알게 되었습니다. 😭
알고리즘 플로이드-워셜(백준 11404, 1389, 11403 -Java)
따라서.... DFS를 사용하기로 했습니다.
먼저 1을 출발노드로 하고 DFS를 사용해보겠습니다.
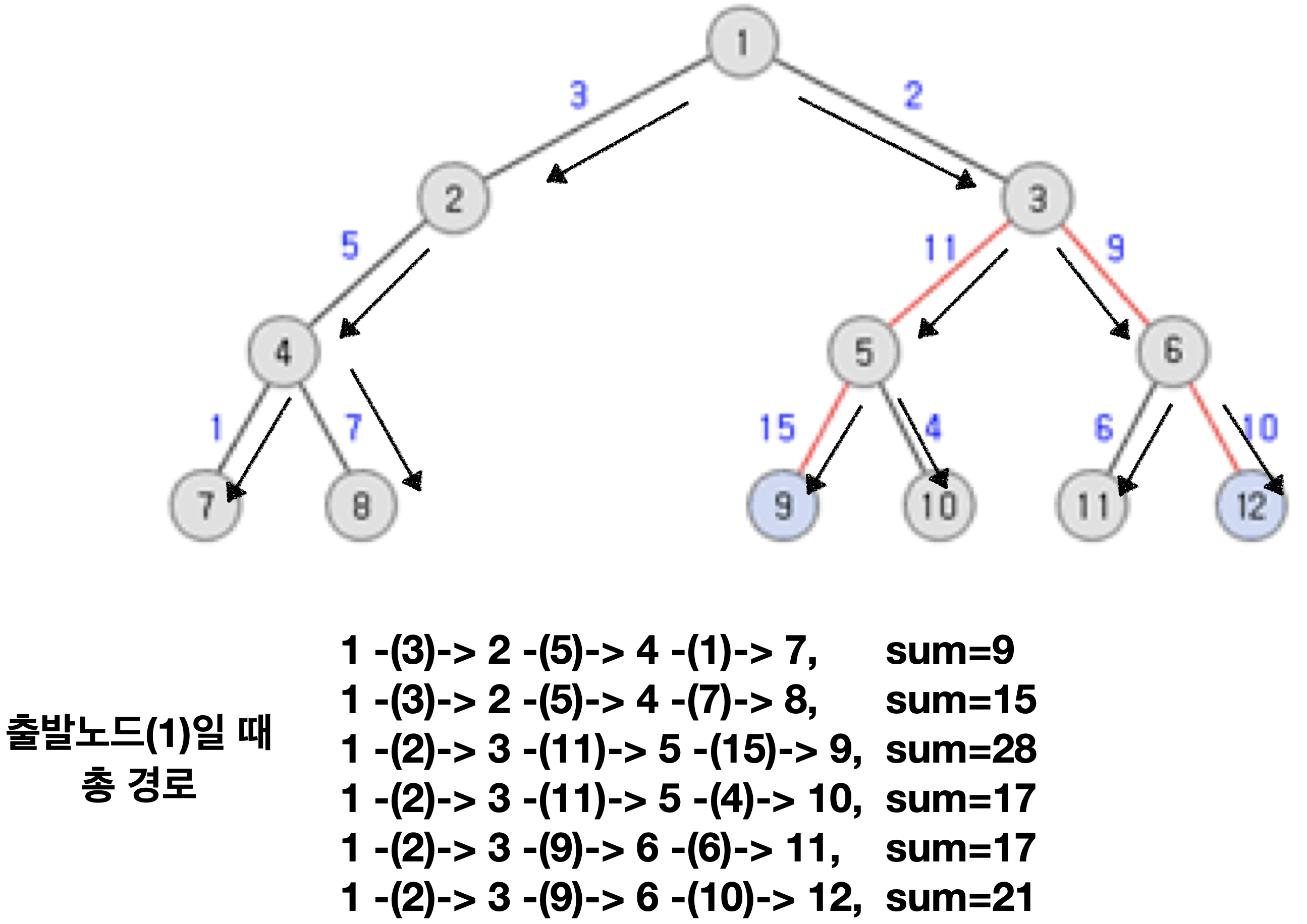
트리는 무방향성, 즉 양방향이라는 것을 기억하셔야 합니다!!
9를 출발 노드라고 하고 DFS를 해보겠습니다.
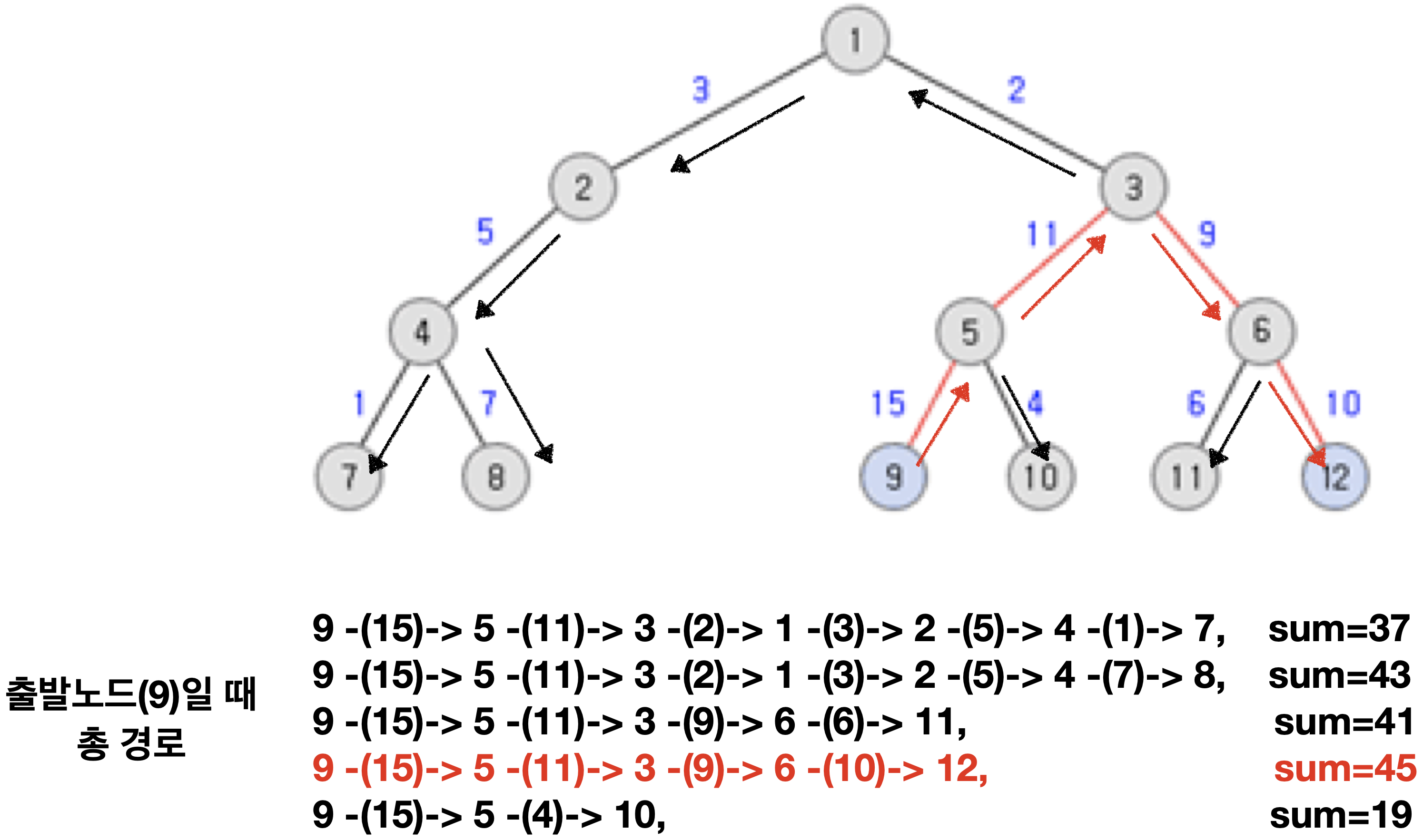
이해가 되시나요?
이를 코드로 구현하면 다음과 같습니다.
여담DFS는 풀어도 풀어도 어려운거 같네요 ㅠ0ㅠ
풀이
public class Quiz1967 {
static int result = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 노드 갯수
int n = Integer.parseInt(br.readLine());
// 트리 초기화
List<Node>[] tree = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
tree[i] = new ArrayList<>();
}
// 트리 생성
for(int i = 1; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int parent = Integer.parseInt(st.nextToken());
int child = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 무방향
tree[parent].add(new Node(child, weight));
tree[child].add(new Node(parent, weight));
}
for(int i = 1; i <= n; i++) {
// 모든점에서 dfs 수행
boolean[] visited = new boolean[n+1];
visited[i] = true;
dfs(tree, visited, 0, i, String.valueOf(i));
}
System.out.print(result);
br.close();
}
private static void dfs(List<Node>[] tree, boolean[] visited, int sum, int start, String path) {
// 시작점에서 인접노드로 탐색
for(int i = 0; i < tree[start].size(); i++) {
// 인접 노드를 꺼낸다.
Node node = tree[start].get(i);
// 인접 노드에 방문한 이력이 없으면
if(!visited[node.getNode()]) {
// 방문
visited[node.getNode()] = true;
// dfs 수행
dfs(tree, visited, sum + node.getWeight(), node.getNode(), path + " -("+node.getWeight()+")-> " + node.getNode());
// 방문 이력 삭제
visited[node.getNode()] = false;
}
}
if(tree[start].size() == 1) {
System.out.println(path+", sum="+sum);
}
result = Math.max(result, sum);
}
static class Node {
private int node;
private int weight;
public Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
public int getNode() {
return node;
}
public int getWeight() {
return weight;
}
}
}
결과

그런데 말입니다..
시간 효율이 너무 안좋은것 같아요…
최소 신장 트리를 이용해볼까?
알고리즘 최소 신장 트리(백준 1197, 1922, 1647, 4386 -Java)
최소 신장 트리는 가중치가 있는 무방향 그래프에서 모든 노드를 연결 할 때 사용된엣지들의 가중치의 합을 최소로 연결하는 트리입니다.
이걸 조금 변형해서 최대로 연결하면 어떨까요? 😁
[알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386 -Java)
[알고리즘] 최소 신장 트리(백준 1197, 1922, 1647, 4386) 알고리즘 공부를 계속 미루는 제 자신을 보고 이대로는 안되겠다 싶어 😇 본격적으로 코딩테스트를 준비(+알고리즘 공부) 해보려고 합니다.
howisitgo1ng.tistory.com
이 방법은 사용할 수 없습니다…!
그 이유는 해당 그래프가 트리이기 때문 입니다.
트리는 이미 최소 간선으로 모든 노드들과 연결되어 있습니다….!
따라서 최소 신장 트리 방법을 이용하면 73이 나오게 됩니다.^^
DFS를 2번만 사용하자!
루트 노드에서 가장 먼 노드를 탐색하고,
가장 먼 노드에서 다시 가장 먼 노드를 탐색하는 방법 입니다.
원리를 그림으로 설명하면 다음과 같습니다.!

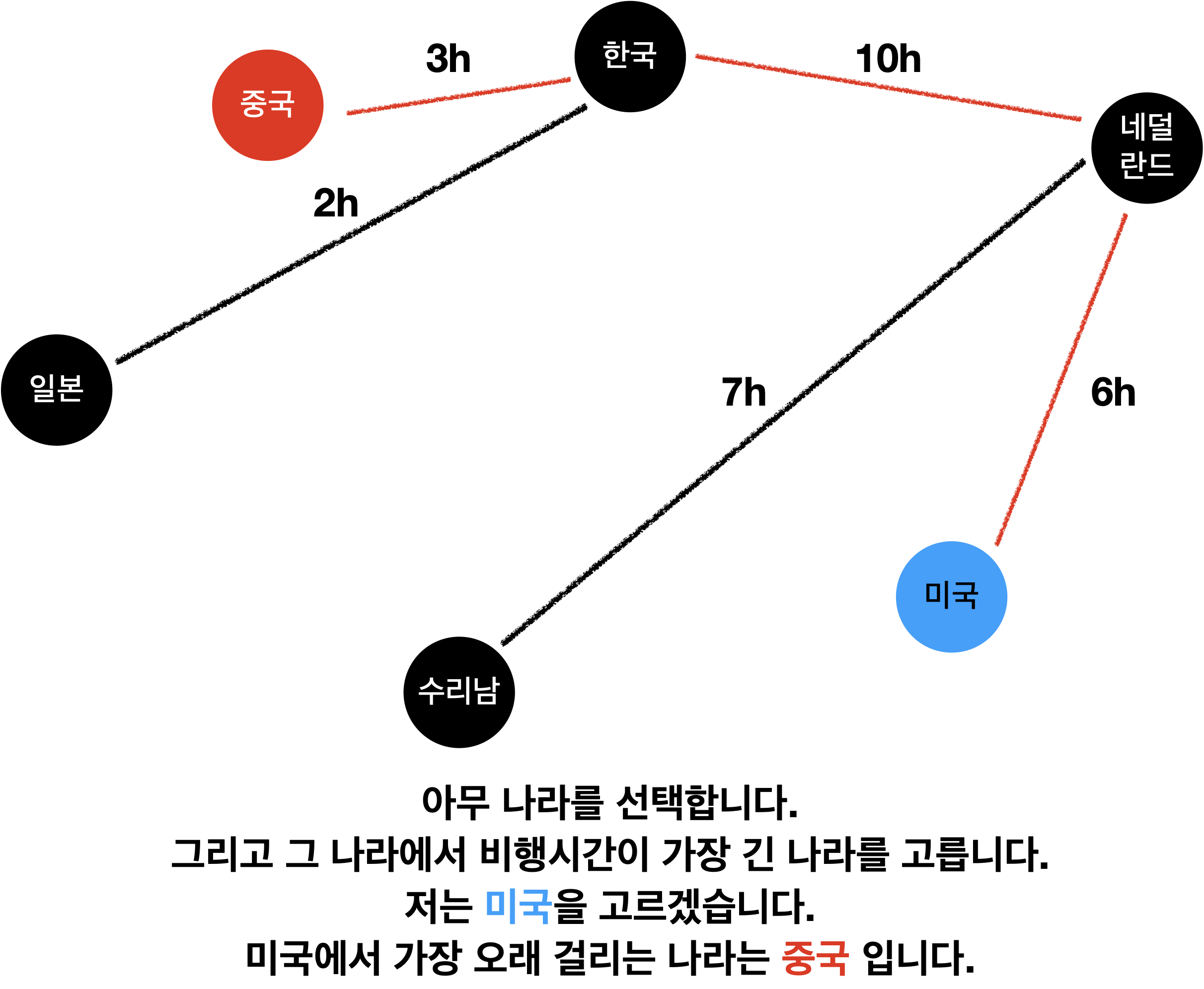
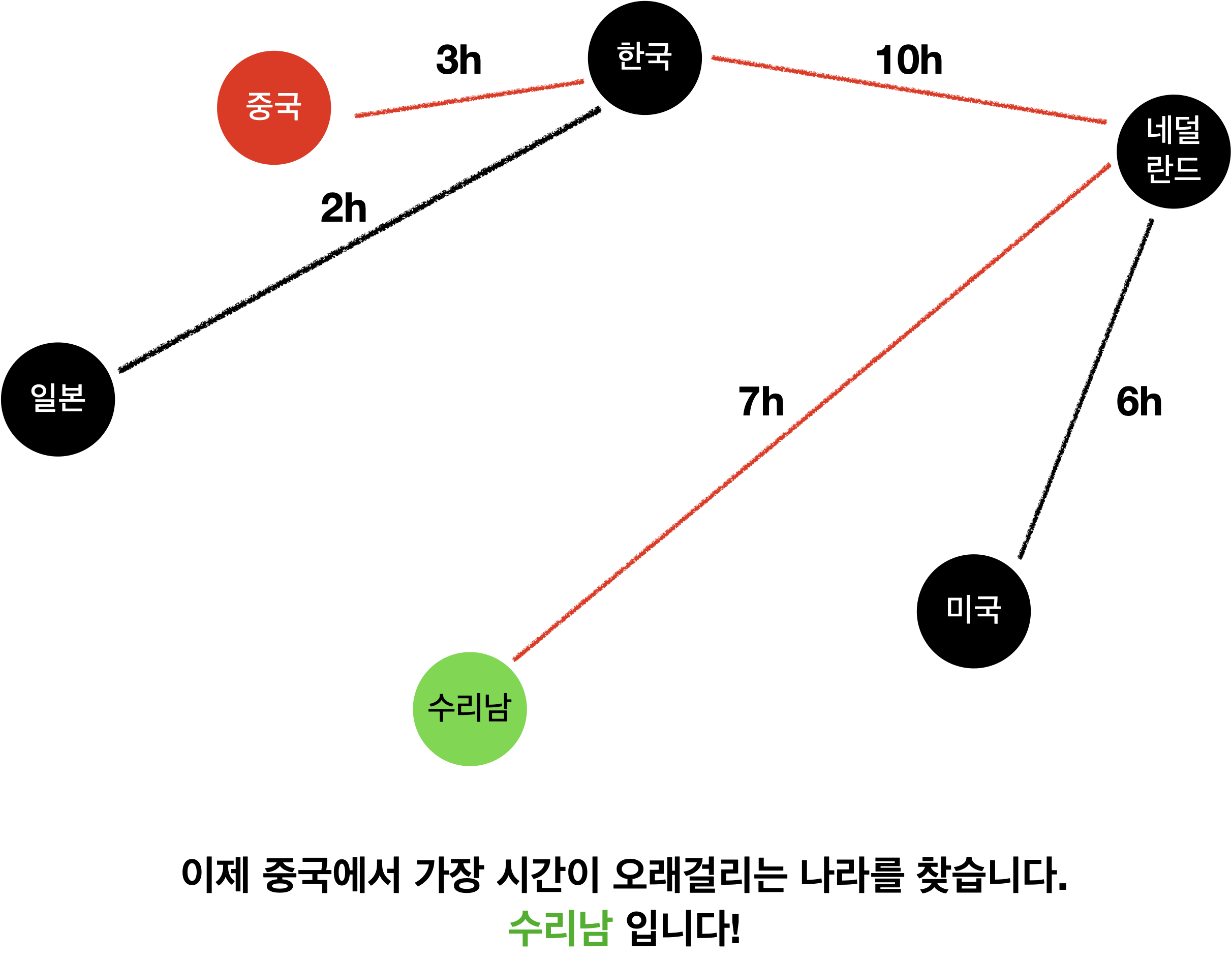
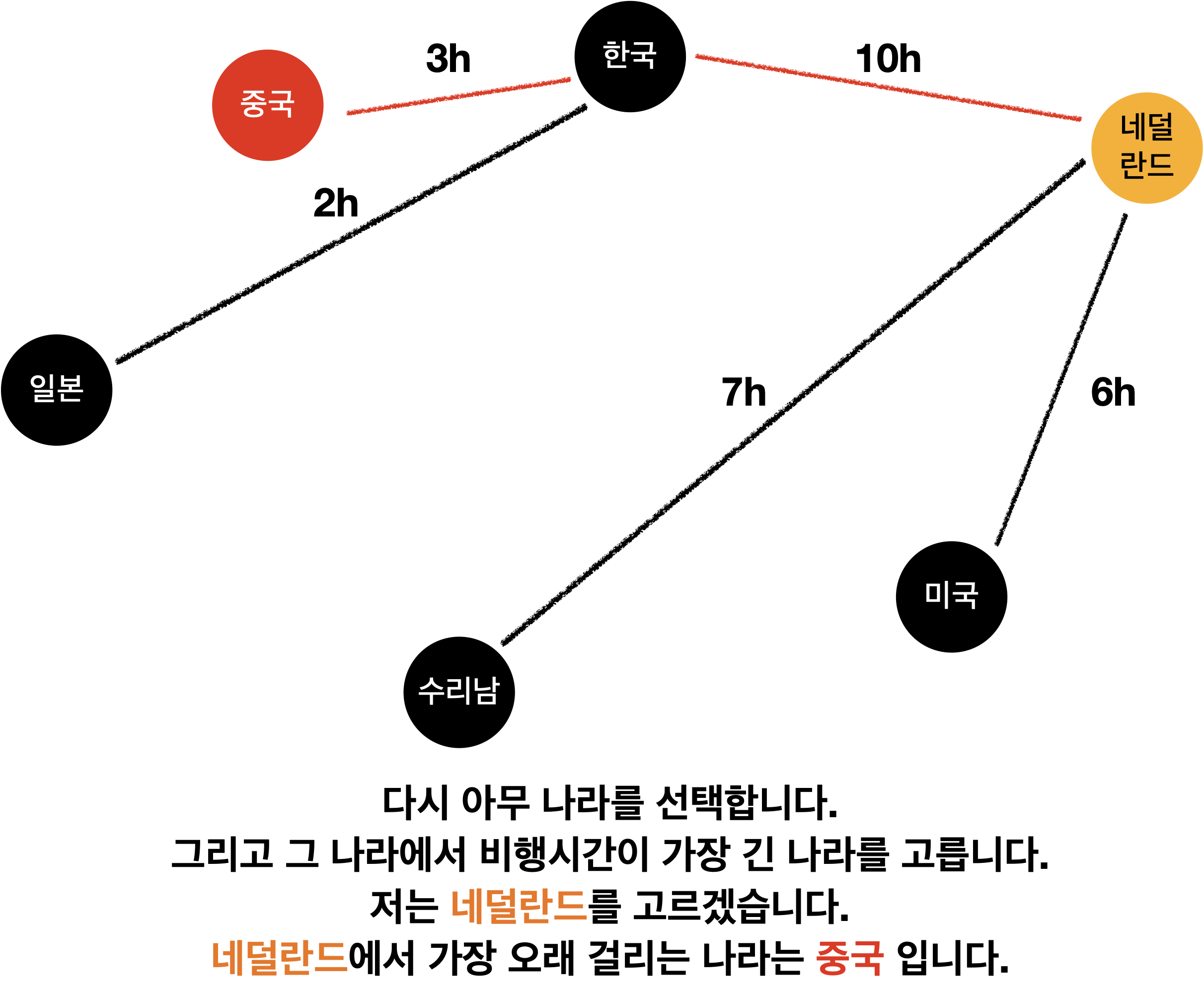
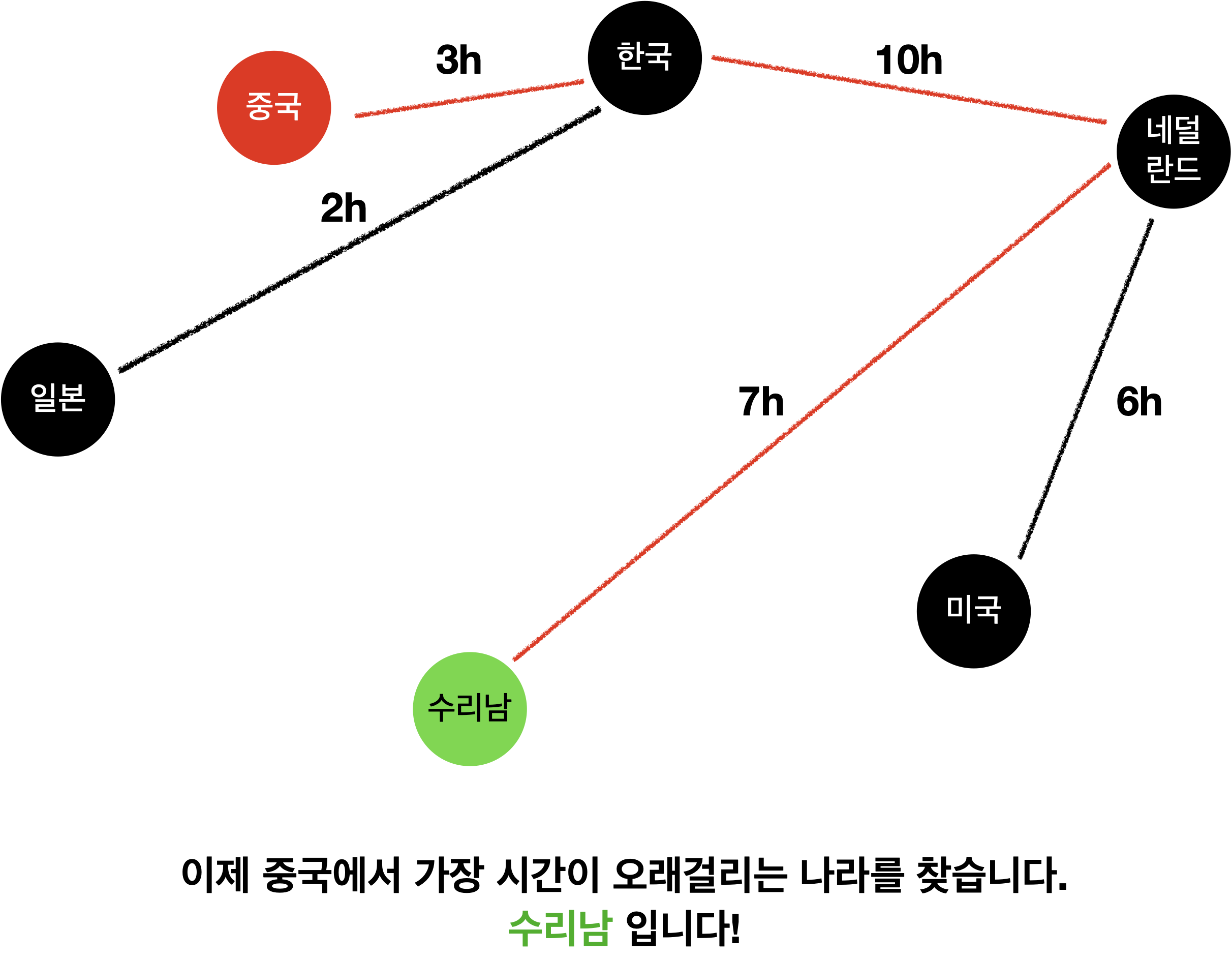
이와 같은 원리로 하면 해결됩니다!
신기하죠?
근데 왜 루트 노드를 선택하나요? 🤔
여기서 루트 노드를 선택하는 이유는 루트 노드는 항상 존재하기 때문입니다!! 😊
루트 노드에서 가장 먼 노드를 찾았으면
그곳에서 가장 먼 노드를 탐색!
솔직히 이런 생각을 어떻게 하는지 모르겠습니다…
알고리즘 고수님들은 정말로 대단합니다.. 👍
풀이
public class Quiz1967_2 {
static List<Node>[] tree;
static boolean[] visited;
static int result = 0;
static int myNode = 0;
public static void main(String[] args) throws IOException {
/**
* 모든 노드 각 노드까지 DFS를 이용하여 최대거리를 구한다.
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 노드 갯수
int n = Integer.parseInt(br.readLine());
// 인접 리스트 초기화
tree = new ArrayList[n+1];
for(int i = 1; i <= n; i++) {
tree[i] = new ArrayList<>();
}
// 인접 리스트 생성
for(int i = 1; i <= n - 1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 무방향 -> 양방향
tree[node1].add(new Node(node2, weight));
tree[node2].add(new Node(node1, weight));
}
// 방문 배열 초기화
visited = new boolean[n+1];
// 첫 번째 노드는 방문 처리
visited[1] = true;
// 아무노드나 선택해도 되지만,
// 루트노드가 항상 존재하는 것을 알기 때문에 루트 노드를 선택
dfs(1, 0);
// 방문 배열 초기화
visited = new boolean[n+1];
// 첫 번째 노드는 방문 처리
visited[myNode] = true;
// 루트노드에서 제일 먼 노드를 찾으면
// 해당 노드에서 가장 먼 노드 까지 거리 탐색
dfs(myNode, 0);
System.out.print(result);
br.close();
}
private static void dfs(int start, int sum) {
// 최대 거리 계산
result = Math.max(sum, result);
if(sum == result) {
// 최대 거리일 때 노드 저장
myNode = start;
}
// 시작점에서 인접노드로 탐색 시작~
for(Node data : tree[start]) {
// 인접 노드 꺼낸다.
int node = data.getNode();
int weight = data.getWeight();
// 방문 이력이 없으면
if(!visited[node]) {
// 방문 처리
visited[node] = true;
dfs(node, sum + weight);
// 모든 노드를 탐색해야하기 때문에 방문 이력 삭제
visited[node] = false;
}
}
}
private static class Node {
private int node;
private int weight;
public Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
public int getNode() {
return node;
}
public int getWeight() {
return weight;
}
}
}
이전 보다 2,500ms 가량 속도가 개선되었습니다!!

정리
- 트리에서 노드 간의 최대 거리를 구할 때는
DFS를 이용한다. - 루트 노드에서 가장 먼 노드를 찾는다.
- 아무 노드나 해도 상관 없음
- 찾은 노드에서 가장 먼 노드까지의 거리를 구한다.
'0 + 알고리즘(Algorithm) > 0 + 백준' 카테고리의 다른 글
| [백준 1987] 알파벳(Java) (0) | 2023.04.16 |
|---|---|
| [백준 2468] 안전 영역(Java) (0) | 2023.04.16 |
| [백준 1260] DFS와 BFS(Java) (0) | 2023.04.15 |
| [백준 16953] A → B(Java) (0) | 2023.04.07 |
| [백준 1504] 특정한 최단 경로(Java) (0) | 2023.04.06 |