https://www.udemy.com/share/105zfq/
해당 포스팅은 JavaScript 알고리즘 & 자료구조 마스터클래스강의를 참고하여 작성했습니다.
빅오(Big-O)

알고리즘은 컴퓨터공학의 🌸꽃이라고 할 수 있습니다.
많은 기업들이 CS 전공지식과 더불어 알고리즘 문제를 입사시험으로 출제 합니다. 그만큼 컴퓨터공학에 있어서 중요하기 때문이겠죠?
그렇다면 알고리즘이란 무엇인가요?
알고리즘은 특정 작업을 달성하기 위한 과정이나 일련의 단계를 의미합니다.
이와 같이 알고리즘은 문제를 해결하기 위해 수행해야하는 수학적 단계라고 정의할수 있습니다.
제 개인적인 의견으로 컴퓨터공학에서 알고리즘이 등장한 이유는 문제 해결에 있어 최고의 성능으로 동작하게 하려고 하는 컴퓨터 과학자, 공학자들의 욕심으로 등장했다고 생각합니다.
문제 해결?
자, 우리는 문제를 해결하는 방법에는 여러가지가 존재한다는 것을 여러분들은 살면서 느꼈을 것 입니다.
컴퓨터 과학자들도 마찬가지입니다.
컴퓨터 과학자들(개발자)은 프로그래밍(알고리즘)을 통해 문제를 해결했습니다.
그런데 말 입니다.🤔
우리는 이것을 정말로 최고로 잘 해결했다고 말할 수 있을까요?
정말로 방금 선택한 알고리즘이 최고의 성능을 자랑하는 것 일까요?
👨🏻🔬의심이 많은 컴퓨터 과학자들은 이러한 문제를 해결하기 위해 알고리즘 성능의 정량적인 척도를 만들었습니다.
그것이 바로 Big-O Notation 입니다.
쉽게 말하면, Big-O Notation은 어떤 알고리즘이 더 좋은지 알기위한 방법입니다.
빅오 표기법의 등장으로 자연스럽게 비효율적인 코드를 찾는데 도움을 주겠죠?
시간 복잡도
최고 성능의 의미는 여러가지로 생각할 수 있습니다.
우리는 크게 2가지로 생각해 봅시다.
- 속도(시간 복잡도)
- 메모리 사용량(공간 복잡도)
입력에 따라서 알고리즘들의 속도가 어떻게 바뀌는지 분석하는 것을 시간 복잡도 분석이라고 합니다.
컴퓨터 사양 또는 애플리케이션의 특성, 환경마다 다르겠지만, 이번에는 속도(시간 복잡도)를 기준으로 알고리즘을 평가 해봅시다!
1 ~ N 까지를 더하는 알고리즘으로 비교해 봅시다.
addUpTo1
for 문을 사용하여 1 부터 N 까지 더합니다.
int addUpTo1(int n) {
int total = 0;
for (int i = 1; i <= n; i++) {
total += i;
}
return total;
}addUpTo2
수학공식(등차수열의 합)을 사용하여 계산합니다.
int addUpTo2(int n) {
// 등차수열의 합
// sum : 결과
// a : 초항
// n : 항의 갯수
// d : 공차
// sum = n(2a + (n - 1)d) / 2
int total = n * (n + 1) / 2;
return total;
}테스트 코드
@Slf4j
public class BigOTest {
@Test
void addUpToTest() {
log.info("result1={}", addUpTo1(1000000000));
log.info("result2={}", addUpTo2(1000000000));
}
int addUpTo1(int n) {
long startTime = System.currentTimeMillis();
int total = 0;
for (int i = 1; i <= n; i++) {
total += i;
}
long endTime = System.currentTimeMillis();
log.info("{}ms", endTime - startTime);
return total;
}
int addUpTo2(int n) {
long startTime = System.currentTimeMillis();
// 등차수열의 합
// sum : 결과
// a : 초항
// n : 항의 갯수
// d : 공차
// sum = n(2a + (n - 1)d) / 2
int total = n * (n + 1) / 2;
long endTime = System.currentTimeMillis();
log.info("{}ms", endTime - startTime);
return total;
}
}결과
15:49:09.132 [Test worker] INFO - 417ms
15:49:09.141 [Test worker] INFO - result1=-243309312
15:49:09.141 [Test worker] INFO - 0ms
15:49:09.141 [Test worker] INFO - result2=-243309312속도를 기준으로 생각했을 때 addUpTo2()가 더 성능이 좋다고 말할 수 있겠습니다.
하지만, addUpTo2()같이 성능이 좋은 알고리즘 addUpTo3()이 있다고 합시다.
둘 다 0ms로 동일하죠.
그래도 그중에서 가장 빠르고 가장 효율적인 코드가 있을 것 입니다.
하지만 현재로서 이러한 작은 속도 차이를 측정하기는 어렵습니다.
기기마다 다른 방식으로 시간을 기록하고, 기기 사양에 따라서 시간 측정 결과가 다를 수 있습니다.(갑자기 addUpTo2()가 addUpTo1() 보다 빨라 질수는 없지만요.)
제가 하고 싶은 이야기는 알고리즘을 연산하는데 걸리는 시간이 변할수 있다는 것 입니다.
제 컴퓨터에서는 0ms가 나왔지만, 승범이 컴퓨터에서는 100ms의 결과가 나올수 있습니다.
따라서 환경에 따라서 변화하지 않는 성능 척도가 필요합니다.
우리는 코드를 비교하는 특정한 값이 필요합니다.
연산갯수
시간을 사용하지 않으면 무엇으로 측정하면 될까요?
질문을 바꿔 보겠습니다.
알고리즘에서 변하지 않는 것은 무엇일까요?
바로 컴퓨터가 처리해야하는 연산 갯수 입니다.
어떤 컴퓨터를 사용하든 연산 갯수는 변하지 않기 때문입니다.
addUpTo2
int addUpTo2(int n) {
// 등차수열의 합
// sum : 결과
// a : 초항
// n : 항의 갯수
// d : 공차
// sum = n(2a + (n - 1)d) / 2
int total = n * (n + 1) / 2;
return total;
}addUpTo2()의 연산 갯수를 세봅시다.total을 수행하기 위해 곱하기(*), 더하기(+), 나누기(/) 가 존재하는 것을 알수 있습니다. n의 값에 상관없이 연산 갯수가 3개 입니다.
addUpTo1
int addUpTo1(int n) {
int total = 0; // =으로 연산갯수 1개
// =로 연산갯수 1개,
//++로 연산갯수 2n개(++는 i에 +1을 하기 때문에 +, =이 있음(i += 1))
// <=로 연산 갯수 n개
for (int i = 1; i <= n; i++) {
// =으로 연산갯수 n개, +로 연산갯수 n개
total += i;
}
return total;
}addUpTo1()의 연산 갯수를 세봅시다.loop안에 total += i;이 있습니다. 등호(=)와 더하기(+) 연산 1번 사용됐습니다.
그런데, loop안에서 연산은 다릅니다. n의 값에 따라서 연산 갯수가 달라지기 때문이죠. n이 5개면 5번의 더하기 연산이 발생하고 5번의 등호 연산이 발생합니다.
또, loop에서 비교연산(<=), 증가연산(++)이 사용됩니다. 이것도 n의 값에 따라서 달라지죠.
loop에 따라서 연산의 갯수가 바뀝니다.🙀
연산의 갯수를 세기가 어려워요!!!!!!!
그래도 연산의 갯수를 세보자면 5n + 2개 라고 할수 있습니다.
Big O
Big O에서는 이렇게 정확한 연산 갯수는 신경쓰지 않습니다.
연산 갯수의 전체적인 추세만 생각하면 됩니다.10n이든 1000000n이든지 상관 없습니다.
중요한건 addUpTo1()은 n이 커질수록 연산의 갯수도 비례하게 증가한다는 것 입니다.
그래서 Big O는 일반적으로 가장 높은 실행 시간을 의미합니다.
Big O는 알고리즘에 실행시간이 어떻게 변하는지 설명하는 공식적인 방법입니다.(대략적으로 숫자를 세는 것을 의미하고, 오로지 전반적인 추세에만 집중합니다.)
입력의 크기와 실행시간의 관계를 설명합니다.(함수가 실행되는 시간이 변하는 관계를 의미합니다.)
addUpTo2
addUpTo2()를 Big O로 표기해봅시다.addUpTo2()는 항상 연산 갯수가 3개 입니다.
따라서 O(1)이라고 표기할수 있습니다.
addUpTo1
addUpTo1()를 Big O로 표기해봅시다.addUpTo1()는 n에 따라서 연산갯수가 증가 합니다.10n, 5n, 10000n인지 신경쓰지 않아도 됩니다. 전반적인 추세만 생각하면 되기 때문입니다.
따라서 O(n)이라고 표기할수 있습니다.
Big-O 연습
이제 배운 내용을 토대로 새로운 알고리즘을 Big O로 표현해보죠.
countUpAndDown
void countUpAndDown(int n) {
log.info("카운트 업 시작!");
for(int i = 0; i < n; i++) {
log.info("i={}", i);
}
for(int j = n-1; j >= 0; j--) {
log.info("i={}", j);
}
log.info("끝!");
}첫 번째 for문을 보면 addUpTo1()에서와 비슷한것을 확인 할수 있겠습니다. 따라서 첫 번째 for문은 O(n)입니다.두 번째 for문을 보면 마찬가지로 addUpTo1()에서와 비슷한것을 확인 할수 있겠습니다. 따라서 두 번째 for문은 O(n)입니다.
O(n)이 2개 입니다.
그러면 2O(n)이라고 하면 될까요?
정답은 아닙니다.
그렇다면 O(2n)일까요?
아닙니다.!
아까도 언급한것 처럼 전반적인 추세만 신경쓰면 됩니다.
따라서 countUpAndDown()은 O(n)으로 표기합니다.
printAllPairs
😵💫아리송 하나요?
그렇다면 한 번만 더 해봅시다.
void printAllPairs(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
log.info("i={}, j={}", i, j);
}
}
}첫 번째로 for문이 보입니다. 앞선 for문과 다르게 for문안에 for문이 있습니다…!
우리는 앞에서 0부터 n까지 증가하는 for문이 O(n)이라는 것을 알게 되었습니다.printAllPairs()은 O(n)안에 O(n)이 있습니다. 중첩되어 있습니다.
중첩은 조금 다릅니다.
n이 3이라고 해봅시다.
- 첫 번째 루프에서 i가 0으로 시작한뒤 바로 두 번째 루프가 실행됩니다.
그리고 j는 0에서 2까지 실행됩니다.(3번 실행 되었습니다.) - 두 번째 루프가 끝나면 다시 첫 번째 루프가 시작됩니다. 이때 i는 1이겠죠? 다시 두 번째 루프로 들어가고 j는 0에서 2까지 실행 됩니다.(3번 실행되었습니다.)
- 세 번째 루프가 끝나면 다시 첫 번째 루프가 시작됩니다. 이때 i는 2겠죠? 다시 두 번째 루프로 들어가고 j는 0에서 2까지 실행 됩니다.(3번 실행되었습니다.)
- i가 3이 되었습니다. 하지만 i는 3보다 작아야 하기 때문에 루프를 탈출합니다.
지금까지 3번, 3번, 3번 실행 되었습니다. n^2번 실행 했네요?!
여기서 우리는 O(n)연산 안에 O(n)연산이 있으면, O(n^2)이 되는것을 알게 되었습니다.(^2는 제곱)
Big-O 표현식 단순화
빅오 표기법 (big-O notation) 이란 :: 인생의 로그캣
빅오 표기법 (big-O notation) 이란
컴퓨터 과학(Computer Science) 에서 알고리즘은 어떠한 문제를 해결하기 위한 방법이고, 어떠한 문제를 해결 하기 위한 방법은 다양하기 때문에 방법(알고리즘) 간에 효율성을 비교하기 위해 빅오(bi
noahlogs.tistory.com
거시적으로, 최악의 경우로 바라보기 👀
표현식을 단순화 할때 명심해야할 점은 당신이 🌏지구 밖 🧑🏻🚀우주에서 📈그래프를 바라본다고 생각하는 것 입니다.
그리고 알고리즘이 최악의 경우일 때를 생각해야 합니다.
(세웅 알고리즘은 O(n^2 + n)인 알고리즘이라고 합시다. 세웅 알고리즘을 Big-O로 표현하면 무엇일까요?
바로 O(n^2) 입니다.)
위 2가지 관점으로 생각하셔야 합니다.
그러면 표현식의 핵심만 보이게 될것입니다.^^
Quiz
정말로 2가지 관점으로 생각하는지 점검해 볼까요?
다음 알고리즘을 Big-O로 표현해 보세요.!
void quiz(int n) {
for(int i = 0; i < Math.min(n, 10); i++) {
log.info("i={}", i);
}
}알고리즘을 거시적으로 그래프를 그려 보세요!
n이 100만 이면? n이 10억이면?
정답은 O(1) 입니다…!
(n이 10보다 작으면 항상 일정한 연산을 수행합니다. 10은 매우 작은 숫자 입니다.)
이러한 관점으로 생각하는 것에 익숙해졌다면,Big O의 복잡도를 생각하는 방법을 구체적으로 설명해드리겠습니다.
(다만 이것이 100% 일치하지는 않습니다.)
- 산수는 상수(
constant)- 덧셈, 곱셈, 나눗셈, 뺄셈을 포함합니다.
- 컴퓨터가 100만 더하기 2를 처리하는 시간과 2 더하기 2를 처리하는 시간은 비슷합니다.
- 변수 할당도 상수(
constant)- 컴퓨터가
int a = 1000;과Long b = 100000000000;을 처리하는 시간은 비슷합니다.
- 컴퓨터가
index또는key를 사용해서 배열요소에 접근하는것도 상수aArray[10000];과bArray[100000000];처럼 배열에 인덱스를 이용해서 접근하는 시간은 비슷합니다.
loop가 있으면 복잡도가loop의 길이 곱하기loop안에 있는 연산들이 됩니다.loop가 0에서 n까지 진행한다면 n이 커질 수록loop가 반복되는 횟수가 증가합니다.- 만약 중첩
loop가 있다면n^2실행시간이 될수 있습니다.
빅오 표기법에서 주로 사용되는 표기법과 그래프는 다음과 같습니다.
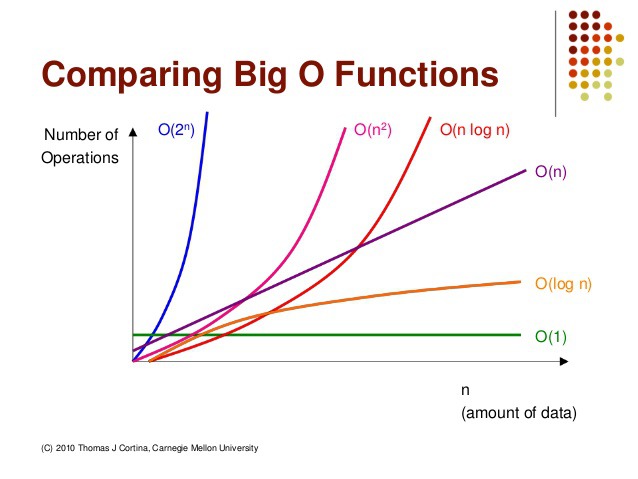
공간 복잡도
최고 성능의 의미로 앞에서는 시간 복잡도를 기준으로 알고리즘을 평가했습니다.
이번에는 입력에 따라서 알고리즘이 어떻게 공간을 차지 하는지 공간 복잡도에 대해서 알아봅시다.
- 속도(시간 복잡도)
- 메모리 사용량(공간 복잡도)
일단 무시해야 하는 사항이 있습니다.
바로 n이 커질수록, 무한대까지 가면서 입력 자체가 커진다는 사항 입니다.
우리는 입력이 차지하는 공간에는 관심이 없습니다.
알고리즘 자체가 필요로 하는 공간에만 관심이 있습니다.
다음 함수를 보면서 설명 드리겠습니다.
Sum
여기서 집중해야 할 것은 바로 입력(arr)에 관심을 두지 않는 것 입니다.
알고리즘 자체가 필요로 하는 공간(메모리)에만 관심을 갖으면 됩니다.
Integer sum(List<Integer> arr) {
Integer total = 0; // 상수 1개
// i: 상수 1개
for(int i = 0; i < arr.size(); i++) {
total += arr.get(i);
}
return total;
}입력의 크기와 관계없이 상수가 2개 입니다.
입력의 크기는 무시합니다….!! 입력이 커질수록 total의 값만 커질 뿐 입니다.
따라서 O(1)이 됩니다.!
getDouble
List<Double> getDouble(List<Double> arr) {
List<Double> newArr = new ArrayList<>();
for(int i = 0; i < arr.size(); i++) {
newArr.add(2 * arr.get(i));
}
return newArr; // 변수 n개
}이 경우는 조금 다릅니다.newArr 배열은 입력의 크기에 따라서 newArr의 크기가 커집니다.
따라서 O(n)이라고 할 수 있습니다.
Logarithm(로그)
우리는 지금까지 O(1), O(n), O(n^2) 같은 빅오 표기법을 배웠습니다.
하지만 어떤 알고리즘은 이처럼 간단하지 않을 수 있습니다.
먼저 우리가 중학교때 배운 로그에 대해서 간단하게 설명하겠습니다.

2를 밑으로 하는 8의 로그는 3과 같다고 할수 있습니다.
이 말은 2를 3제곱하면 8 이라고 하는 것과 같습니다.
이것을 일반화 하면 다음과 같습니다.

2를 밑으로 하는 값(value)의 로그는 지수(exponent)가 되고, 2의 지수(exponent)제곱은 값(value) 입니다.
거시적인 관점에서 바라보면 밑은 의미가 없습니다.
따라서 다음과 같이 생각할수 있습니다.! (10이 밑인 로그는 10을 생략합니다.)
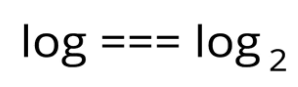
정리
- 알고리즘의 성능을 분석하기 위해서는
Big-O표기법을 사용합니다.- 우리가 궁금한것은 알고리즘의 시간 복잡성과 공간 복잡성 입니다.
Big-O표기법으로 우리는 컴퓨터 하드웨어의 영향을 받지 않습니다.- 실행될 연산의 갯수를 따지기 때문입니다.
- 다시 돌아와서, 결국에는 우리는 아래의 그래프를 인지하고 있으면 됩니다.
- 시간 복잡성, 공간 복잡성의 정확성이 아니라 전체적인 추세만 기억하면 됩니다.
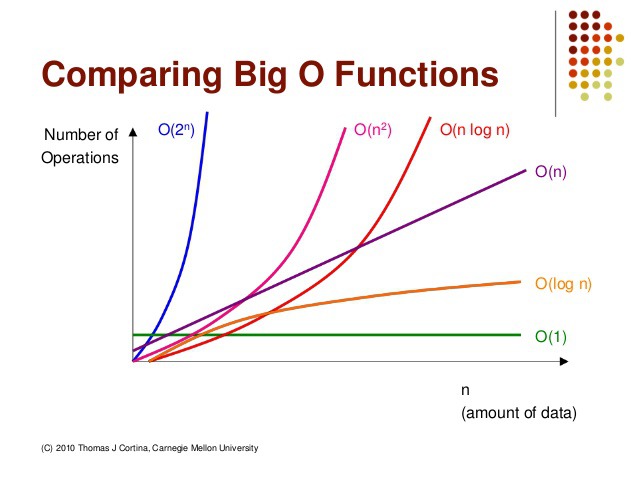
🎉 축하합니다!!
이제 Big-O 표기법을 이용해서 알고리즘의 시간 복잡도와 공간 복잡도를 이야기 할수 있겠죠?
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 배열과 리스트(백준 11720, 1546) (0) | 2023.03.06 |
|---|---|
| [알고리즘] 재귀(Recursion -java) (1) | 2023.01.28 |
| [알고리즘] 슬라이딩 윈도우 패턴(Sliding Window -java) (0) | 2023.01.27 |
| [알고리즘] 다중 포인터 패턴(Multiple Pointers -java) (2) | 2023.01.27 |
| [알고리즘] 빈도수 세기 패턴(Frequency Counters -java) (0) | 2023.01.22 |