[알고리즘] 재귀(Recursion)
JavaScript (JS) Algorithms and Data Structures Masterclass | Udemy
해당 포스팅은 JavaScript 알고리즘 & 자료구조 마스터클래스강의를 참고하여 작성했습니다.
재귀는 자기 자신을 호출하는 절차 입니다.
🤔 이해가 잘 되지 않는다고요?
옛날 옛적에 🧙민혁이라는 초보 마법사가 있었습니다.
그 당시에는 컴퓨터가 없어서 홀수와 짝수를 구분할 수 없었는데,
민혁이는 🧙♂️스승님에게 마을에 있는 🐉용에게 가서 홀수와 짝수를 구분해오라는 퀘스트를 받습니다.
스승님에게 받은 종이에는 다음과 같이 쓰여져 있었습니다.
(112, 12344, 6764, 11238)
종이를 갖고 용집에 도착한 민혁이는 용에게 가서 부탁했습니다.
용님 홀수와 짝수좀 구분해주세요.
용이 말했습니다.
아 오늘은 내가 좀 바쁘니까 첫번째 목록에만 있는 숫자만 홀수인지 짝수인지 알려줄께.
민혁이는 당황해 하며, 용님 다 알려주시면 안될까요?
용이 소리치며 말했습니다.
아 오늘은 좀 바쁘다고! 그것도 알기 싫으면 돌아가!
깜짝 놀란 민혁이는 그 순간 좋은 방법이 생각 났습니다.
민혁이는 첫 번째 종이를 내밀었습니다.
(112, 12344, 6764, 11238)
용이 말했습니다. 음 짝수야.
민혁이는 두 번째 종이를 내밀었습니다.
(12344, 6764, 11238)
용이 말했습니다. 음 짝수야.
민혁이는 세 번째 종이를 내밀었습니다.
(6764, 11238)
용이 말했습니다. 음 짝수야.
민혁이는 네 번째 종이를 내밀었습니다.
(11238)
용이 말했습니다. 음 짝수야.
웃으며, 🐲용이 말했습니다.!
이녀석! 드디어 재귀에 대해서 깨달았구나!!

호출 스택(Call Stack)
거의 모든 프로그래밍 언어에는 보이지 않는 곳에서 함수 호출을 관리하는 일종의 데이터 구조가 있습니다.
호출된 함수는 다른 함수가 반환(return)될 때까지 기다리는 경우가 많습니다.
함수가 무작위로 실행될 수는 없기 때문이죠.
제일 먼저 호출한 함수가 있고, 그 함수 안에서 두 번째 함수를 호출합니다.
함수가 올바른 순서대로 실행되어야 합니다.
그래서 이걸 담당하는 데이터 구조가 있는데java의 경우 호출 스택(call stack)입니다.
간단하게 JVM 영역에 대해서 언급 하겠습니다.
- 메소드 영역(
Method Area)- 클래스 정보와 클래스 변수가 저장되는 곳
- 호출 스택(
Call Stack)- 메소드의 작업 공간
- 메소드가 호출되면 호출 스택 메모리에 할당
- 메소드 호출이 종료되면 사용하던 메모리 반환
- 힙(
Heap)- 인스턴스가 생성되는 공간
new 연산자에 의해 생성되는 배열, 객체는 모두 여기에 생성!
CallStack
public class CallStack {
public static void main(String[] args) {
hello();
}
public static void hello() {
bye();
}
public static void bye() {
System.out.println("bye");
}
}호출 스택 과정이 어떻게 진행되는지 그림으로 표현하면 다음과 같습니다.
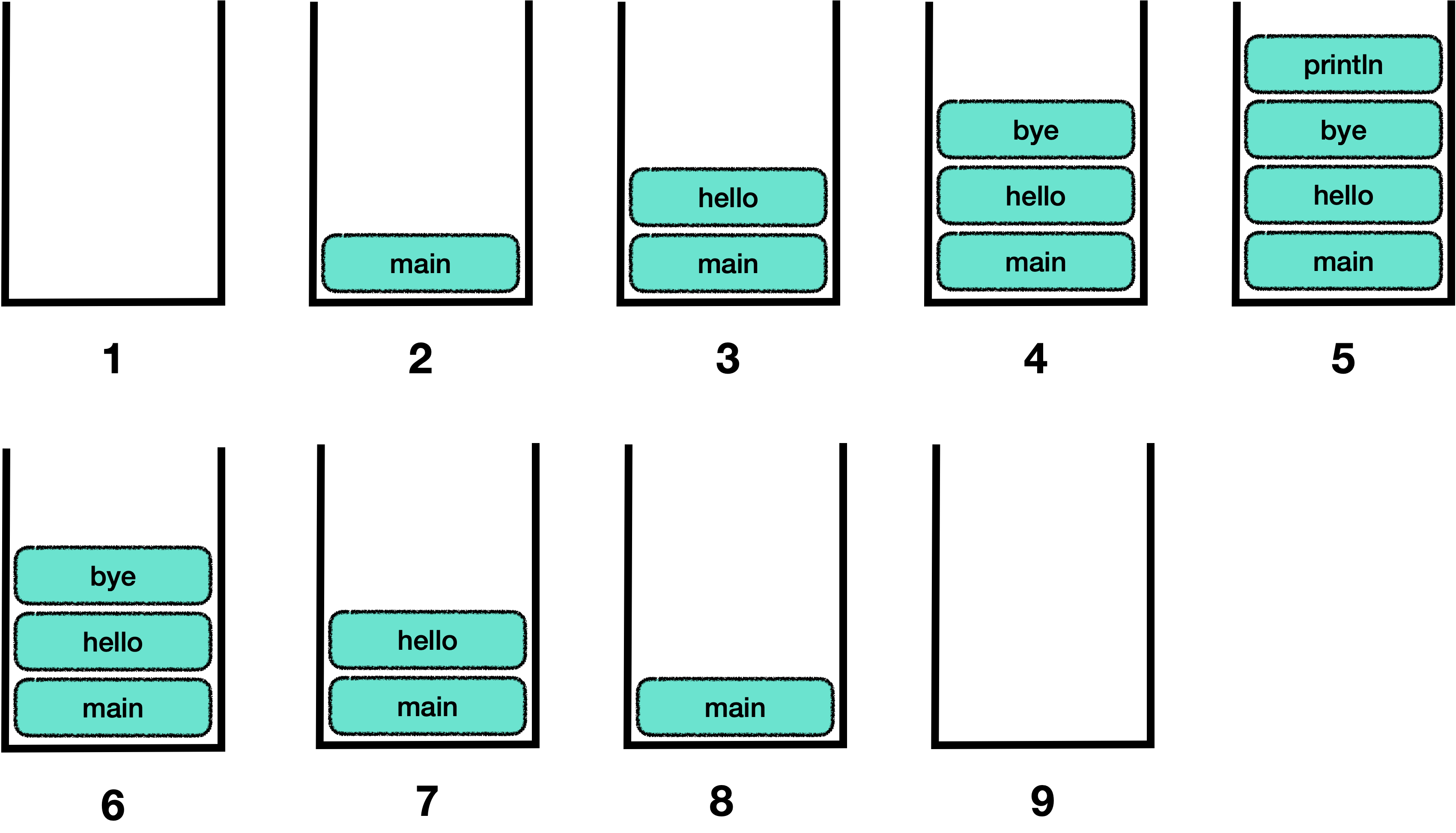
호출 스택을 알아본 이유는 우리가 재귀함수를 작성할 때
호출 스택을 엄청나게 많이 사용하게 될 것이기 때문입니다….!
재귀 함수
어떤 재귀 함수든 반드시 갖춰야 하는 2가지 요소가 있습니다.
base case- 종단점
- 자기자신을 호출하는 것은 영원히 계속되면 안된다.
different input- 다른 입력값
- 자기자신을 호출할 때 입력값이 달라진다.
먼저 간단한 재귀함수를 한 번 살펴봅시다.
countDown
void countDown(int num) {
if(num <= 0) {
System.out.println("All Done");
return; // base case
}
System.out.println(num);
num--;
countDown(num);
}
// num = 3 일때
// print 3
// countDown(2)
// print 2
// countDown(1)
// print 1
// countDown(0)
// print "All Done"
// return;주석과 같은 방식으로 실행되는 것을 알수 있습니다.
또 다른 예를 보시죠.
sumRange
int sumRange(int num) {
if(num == 1) {
return 1; // base case
}
return num + sumRange(num - 1);
}
// num = 3 일때
// return 3 + sumRange(2)
// return 2 + sumRange(1)
// return 1num이 커질 수록 stack call에서 배운 내용처럼stack에 많은 함수들이 쌓이는 것을 알수 있습니다.(sumRange의 반환값을 기다리고 있습니다.)
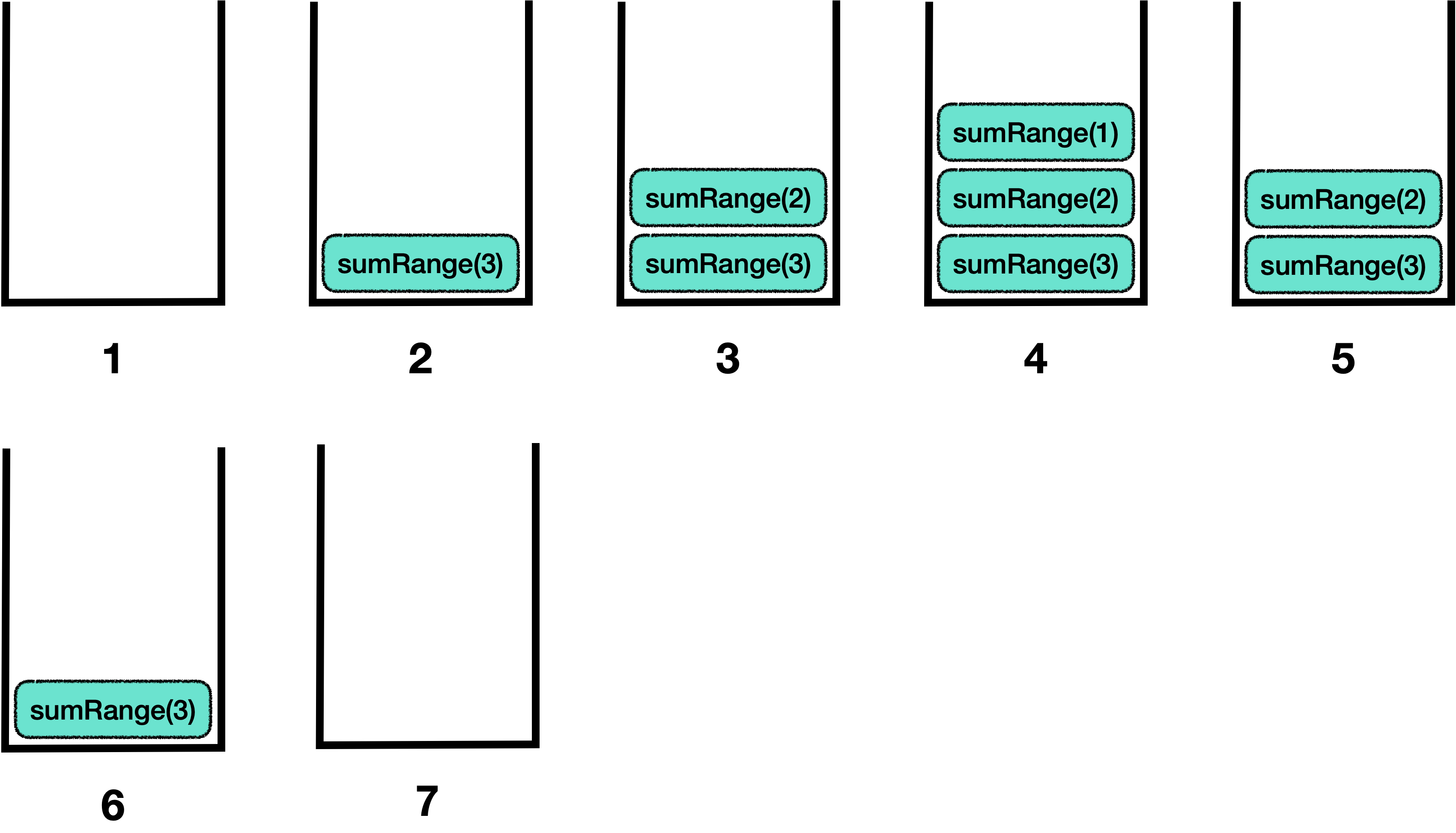
이번에는 재귀 연습을 할 때 가장 흔히 사용 되는 팩토리얼 함수를 작성해 봅시다.
factorial
int factorial(int num) {
if(num == 1) {
return 1;
}
return factorial(num - 1) * num;
}
// num = 3 일때
// return 3 * factorial(2)
// return 2 * factorial(1)
// return 1재귀의 함정(StackOverflowError)
재귀의 함정은 종료 조건이 없거나 잘못되는 경우를 들수 있습니다.
방금 작성한 팩토리얼로 예를 들면 다음과 같습니다.
코드가 계속 실행되면서 스택에 계속해서 함수를 추가합니다.
만약 num이 무한으로 큰 값이면 어떤 결과를 초래할까요?
또 base case를 잘못 작성하면 어떻게 될까요?
메모리가 터져버릴수 있습니다. 🙀
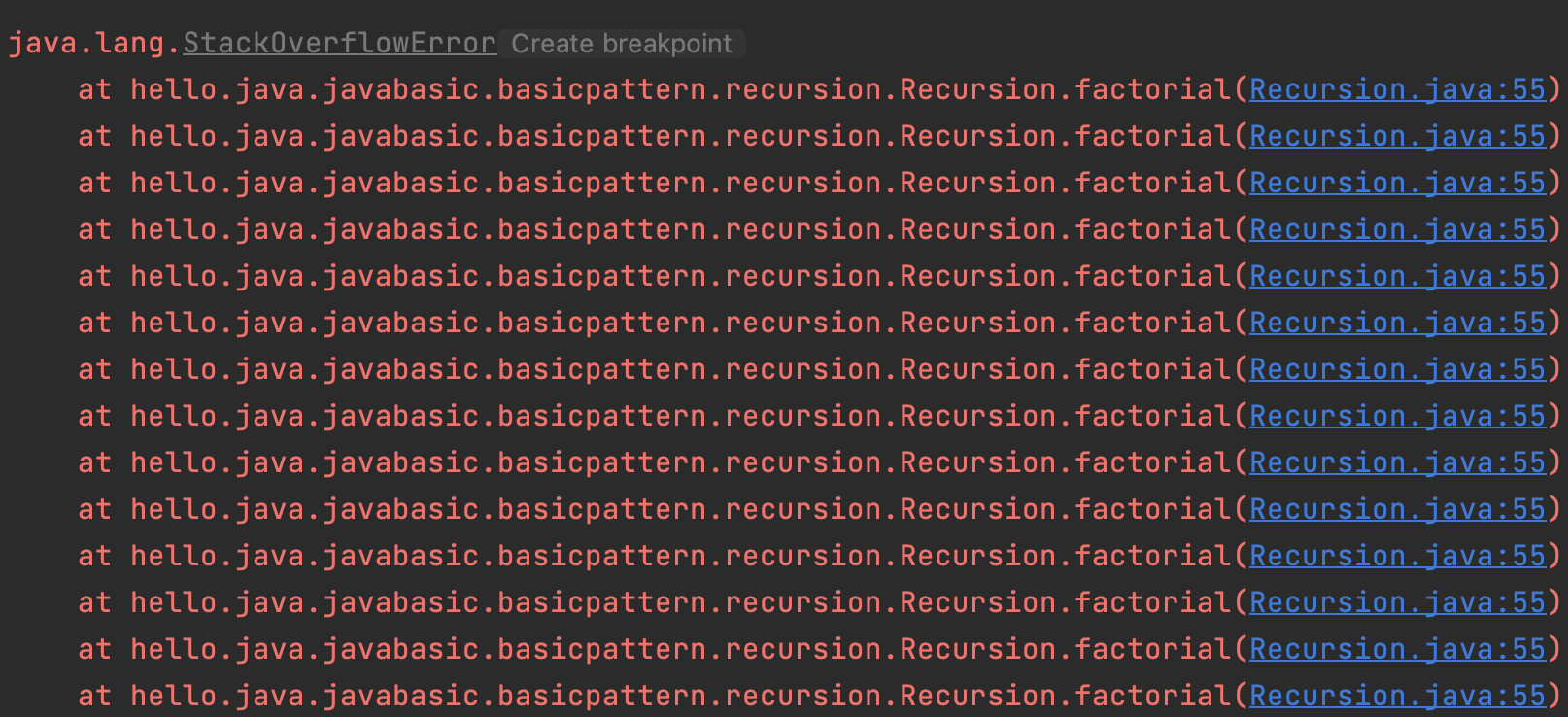
일반적으로 java.lang.StackOverflowError가 발생하면 재귀 코드에 버그가 있다는 신호입니다.
call stack은 모든 항목이 서로에게 의존하면서 계속 대기하는 것 입니다.
띠처럼 연결되어 있다고 생각하면 됩니다.
마지막에는 어떤 값을 도출해서 그 값을 돌려보내야 합니다.
✅ 명심하세요!
종료조건이 없는 경우, 값을 반환하는 것을 잊은 경우, 잘못된 값을 반환하는 경우가 java.lang.StackOverflowError을 야기할수 있습니다.!
헬퍼 메소드 재귀(Helper Method Recursion)
지금까지 우리가 작성했던 모든 재귀함수는 factorial처럼 단일 단독 함수(single standalone function) 였습니다.
헬퍼 메소드 재귀는 조금 다릅니다.
헬퍼 메소드 재귀에는 2개의 함수가 있습니다.외부 함수, 재귀 함수 이렇게 2개 있습니다.
재귀적이지 않은 외부 함수가 재귀적인 내부함수를 호출하는 패턴 입니다.
HelperMethodRecursion
public class HelperMethodRecursion {
@Test
void test() {
System.out.println(collectOddValues(new int[]{1, 2, 3, 4, 5}));
}
List<Integer> collectOddValues(int[] arr) {
List<Integer> result = new ArrayList<>();
helper(arr, result);
return result;
}
List<Integer> helper(int[] helperInput, List<Integer> result) {
if(helperInput.length == 0) {
return result;
}
if(helperInput[0] % 2 != 0) {
result.add(helperInput[0]);
}
int[] sliceArray = Arrays.copyOfRange(helperInput, 1, helperInput.length);
return helper(sliceArray, result);
}
}재귀적이지 않은 외부 함수(collectOddValues)가 재귀적인 내부함수(helper)를 호출하는 패턴 입니다.
collectOddValuesPureRecursion
public class HelperMethodRecursion {
@Test
void test() {
//System.out.println(collectOddValues(new int[]{1, 2, 3, 4, 5}));
System.out.println(collectOddValuesPureRecursion(new int[]{1, 2, 3}));
}
List<Integer> collectOddValuesPureRecursion(int[] arr) {
List<Integer> result = new ArrayList<>();
if(arr.length == 0) {
return result;
}
if(arr[0] % 2 != 0) {
result.add(arr[0]);
}
int[] sliceArray = Arrays.copyOfRange(arr, 1, arr.length);
result.addAll(collectOddValuesPureRecursion(sliceArray));
return result;
}
// collectOddValuesPureRecursion([1, 2, 3])
// result=[1], [1].addAll(collectOddValuesPureRecursion([2, 3]))
// result=[], [].addAll(collectOddValuesPureRecursion([3]))
// result=[3], [3].addAll(collectOddValuesPureRecursion([]))
}이번에는 순수하게 재귀만 사용해서 작성한 코드 입니다.
정리
- 재귀는 자기 자신을 호출하는 절차 입니다.
- 재귀를 사용할 때는
base case,different input에 주의해야 합니다.- 종료조건이 없는 경우, 값을 반환하는 것을 잊은 경우, 잘못된 값을 반환하는 경우
call stack에 무한정으로 쌓이면stackOverflow발생
- 종료조건이 없는 경우, 값을 반환하는 것을 잊은 경우, 잘못된 값을 반환하는 경우
- 헬퍼 메소드 재귀 패턴(
Helper Method Recursion)을 고려해보면 좋습니다.- 재귀적이지 않은 외부함수가 재귀적인 내부함수를 호출하는 패턴
'0 + 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 구간 합(백준 11659, 11660 -Java) (0) | 2023.03.08 |
|---|---|
| [알고리즘] 배열과 리스트(백준 11720, 1546) (0) | 2023.03.06 |
| [알고리즘] 슬라이딩 윈도우 패턴(Sliding Window -java) (0) | 2023.01.27 |
| [알고리즘] 다중 포인터 패턴(Multiple Pointers -java) (2) | 2023.01.27 |
| [알고리즘] 빈도수 세기 패턴(Frequency Counters -java) (0) | 2023.01.22 |